Minimisation fonction.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
par Deluxor » 04 Juin 2013, 16:53
Bonsoir!!
Je cherche à comprendre la correction d'un exercice de minimisation d'une fonction.
Soit
une matrice
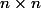
symétrique définie positive.
A tout
on associe la fonction
définie sur
par :
 \, = \, \frac{1}{2}.x^T.A.x \, - \, y^T.x)
.
1. Prouver que
atteint son minimum sur
.
On montre pour cela que
est coercive sur
.
Par Cauchy-Schwarz :
 \, \geq \, \frac{1}{2}.\lambda.N_2^2(x) \, - \, N_2(x).N_2(y))
, avec
la plus petite valeur propre strictement positive de
. (
comment retrouver cela?)
Donc
 \, \to \, +\infty)
lorsque
=\sqrt{\bigsum_{i=1}^n \, x_i^2} \, \to \, +\infty)
.
2. Déterminer le point critique
de la fonction.
On résout :
 \, = \, A.\hat x \, - \, y = 0)
Comment trouve-t-on cette dérivée?Je vous remercie =)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
