Méthodes d'intégration numérique

[ludo56]

Bonjour,alors j'ai un petit problème concernant les hypothèses dans les théorèmes donnant les erreurs d'approximation.
Par exemple,la méthode des rectangles à un pas:on approche l'intégrale d'une fonction f entre a et b par l'intégrale de la fonction constante .
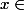
Le théorème dit alors que si est de classe sur [a,b], alors l'erreur est majorée par avec le sup pour de |f'(x)|
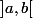
Or j'ai l'impression que l'hypothèse f continue sur et dérivable sur est suffisante pour aboutir,le cœur de la preuve étant l'utilisation du théorème des accroissements finis. Et il en est de même pour la méthode des rectangles,ou encore de Simpson...Je suppose cependant que ces hypothèses doivent être utile mais je ne vois pas ou.
Merci d'avance pour vos éclaircissement.

[dudumath]

Le sup de f' peut-être atteint sur [a,b], or si f n'est que dérivable, et pas C1, la dérivée n'est pas forcément continue et donc n'a éventuellement pas de sup

[Ben314]

Aprés, si on veut faire le "méga super pédant", effectivement, si on suppose f dérivable, f' par forcément continue mais que l'on rajoute comme hypothèse que |f'| est majorée par M, le résultat du théorème reste valable...

Aprés, vu l'idée que je me fait de l'utilité des méthodes numériques, je pense pas que le théorème soit plus interessant sous cette nouvelle forme...

[ludo56]

D'accord,merci à vous deux.
Les méthodes numériques ont quand même leurs importance! D'autant plus dans la vie de tout les jours..

[Ben314]

Bien que ça ne me passionne pas (les gout et les couleurs...), je n'ai absolument pas voulu dire que le théorème était "ininteressant" ou "inutile", mais seulement qu'à mon avis, dans le domaine du calcul numérique, on ne doit pas utiliser fréquement des fonctions dérivables dont la dérivée n'est pas continue (peut-être me trompe-je...)
Cela signifiait simplement que je pense que ta "généralisation" du théorème, bien que mathématiquement juste, n'est pas super utile dans la pratique...

Par exemple, à mon avis, il est bien plus interessant de voir que le théorème continue (évidement) à fonctionner pour des fonctions uniquement C1 par morceaux (et pas forcément continues) ce qui permet de l'utiliser pour des fonction de "signal".