Méthode RSA

[ludo56]

Bonjour,je suis en train de lire un sujet concernant la méthode RSA,je ne comprends pas un passage:
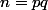
Soit et qui à associe et et qui à associe ( avec et premiers premier avec et l'inverse de modulo )
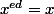
Il est écrit que et sont des bijections réciproque,i.e modulo et la justification est la suivante (je cite) :"il suffit de vérifier l'égalité modulo et modulo en utilisant le petit théorème de Fermat et d'appliquer le théorème chinois."
Il n'y a pas assez de précisions pour que je puisse comprendre!
Votre aide est la bienvenue d'autant plus que ce sujet me passione!
Merci d'avance!

[Nightmare]

Salut !

Par définition, , donc

Reste à montrer que . Ceci est le théorème d'Euler. Si on ne le connait pas, on peut procéder comme le propose l'énoncé, ie de montrer d'abord que et d'utiliser le théorème Chinois.

[ludo56]

Salut!
Pour applique Euler,ne faut-il pas que x et n soit premiers entre eux?

[Ben314]

Si, tout à fait, mais ici ça marche quand même :
Pour tout premier avec p tu as donc, pour tout et donc, pour tout pas forcément premier avec p tu as (puisque si les deux cotés de la congruence sont nuls modulo p).
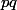
De même pour tout tu as et tu en déduit bien que , que soit premier avec ou pas.

[ludo56]

D'accord bien compris.Merci à vous deux :happy3: