Méthode de Newton

[leeri]

Bonsoir,
J’ai un dm à rendre pour la rentrée et cela fait déjà un bout de temps que je bloque complètement sur une question, je ne dirais pas non à un peu d’aide. La question problèmatique est la I.2)a), je joints le sujet à la fin.
Merci d’avance à ceux qui prendront le temps de me répondre!
https://share.icloud.com/photos/0OTD6jv ... 3Hl9PkkqUg

[LB2]

Bonjour,

c'est vrai que c'est une question un peu abrupte et il faut la prendre par le bon bout pour aboutir.

Tu peux commencer par trouver une relation de récurrence :
exprime la quantité au rang n+1 en fonction de la quantité au rang n.
A savoir ici, calcule et essaie de l'exprimer en fonction (idéalement) de

[Ben314]

Salut,
Perso, plutôt que d'y aller "en tâtonnant" (i.e. en essayant de "faire apparaître miraculeusement" un certain truc), ben j'essayerais plutôt la méthode on ne peut plus naturelle dans un tel cas, à savoir d'inverser le changement de variable.
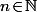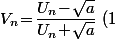Plus précisément, si pour tout tu pose , ben ça semble plus que pas con de commencer par déterminer en fonction de (ce qui ici est immédiat)
Et ensuite, ben c'est complètement mécanique :
- Tu écrit en fonction de gràce à (1).
- Tu utilise la formule donnant en fonction de pour en déduire en fonction de .
- Enfin tu utilise la formule (2) donnant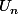 en fonction de pour en déduire en fonction de .

Et j'ai vraiment, mais alors vraiment jamais compris les bricolages infâmes qu'on fait faire aux élèves de Lycée dans ce type de contexte pour montrer (par exemple) que la nouvelle suite obtenue est géométrique.
Il me semble quand même que le B-A-BA de la logique dans ce type de contexte de conversion par exemple entre Degré Celcius et Degré Fahrenheit, ben c'est évidement de commencer par écrire les deux formules de conversions Degré Celcius -> Degré Fahrenheit et Degré Fahrenheit -> Degré Celcius, non ?

Est ce que c'est considéré comme "trop compliqué" pour un Lycéen d'un baccalauréat dit "scientifique" (sic...) de comprendre que si on a une formule du style "température de départ => température d'arrivée" mais où les températures sont exprimées en Degré Fahrenheit, ben pour avoir la même formule où les deux températures sont exprimées en Degré Celcius, il faut faire TROIS opérations (une conversion ; la formule puis une conversion dans l'autre sens) ?

La seule raison que je vois, c'est que ça risquerais de leur faire entrevoir ce qu'est la notion générale de bijection alors qu'on ne compte pas leur balancer la formule théorique de ce que c'est. Faire entrevoir l'utilité d'un concept avant de balancer des formules à apprendre par cœur c'est évidement totalement inadmissible.

[LB2]

@Ben Je suis d'accord avec toi, je pense qu'il serait bon de donner l'intuition du "principe du parapluie" dans de multiples exemples en maths
https://www.youtube.com/watch?v=xrxNhYNUzKI