La méthode de Newton-Raphson
30 messages
- Page 1 sur 2 - 1, 2
la méthode de Newton-Raphson
Bonjour , je dois trouver par la méthode de Newton-Raphson, la solution de léquation : sin(x) = ln(0.5x)
Je sais comment faire mais je sais pas comment avoir la première valeur le X0 , pour le trouver j'ai utlisé la calculatrice et j'ai fais un graph mais je pense pas que ce soit la bonne idée .
Merci pour vôtre aide
Je sais comment faire mais je sais pas comment avoir la première valeur le X0 , pour le trouver j'ai utlisé la calculatrice et j'ai fais un graph mais je pense pas que ce soit la bonne idée .
Merci pour vôtre aide
bonjour
Hyp: l'équation f(x)=0 a une solution.
La suite) converge vers cette solution (dans les bons cas)
converge vers cette solution (dans les bons cas)
}{f'(x_n)})
il fut choisir la valeur initiale non loin de la racine
non loin de la racine
ici,=sin(x)-ln(x)+ln(2))
=cos(x)-\frac{1}{x})
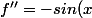+\frac{1}{x^2})
=+\infty; \qquad f(+\infty)=-\infty)
il y a au moins une racine.
lien
Hyp: l'équation f(x)=0 a une solution.
La suite
il fut choisir la valeur initiale
ici,
il y a au moins une racine.
lien
feliraf a écrit:Bonjour , je dois trouver par la méthode de Newton-Raphson, la solution de léquation : sin(x) = ln(0.5x)
Je sais comment faire mais je sais pas comment avoir la première valeur le X0 , pour le trouver j'ai utlisé la calculatrice et j'ai fais un graph mais je pense pas que ce soit la bonne idée .
Merci pour vôtre aide
salut
Le mieux est de choisir un intervalle contenant la solution, sur lequel les dérivées première et seconde ne s'annulent pas, la concavité de la courbe restant la même sur cet intervalle.
Par exemple, on peut prendre la valeur initiale sur [2,6;2,9].
On peut choisir
feliraf a écrit:Je suis d'accord avec vous mathelot pour la méthode mais je vois pas comment on obtient le X0 ?
chan79 j'ai pris un intervalle le même il me semble mais comment le justifier par le calcul , moi j'ai pris ma calculatrice et j'ai fais un graph dessus
les conditions de Dieudonné sont :
soit
quelques soient les points
i)
ii)
alors c bon, on a "existence" et "unicité" de la racine et convergence de la suite
vers cette racine.
grosso modo, il faut que f'(x) ne s'approche pas de zéro ni que f' varie trop.
Ne te prends pas la tête : il n'y a pas de méthode générale pour choisir x0.
Tu en prends un "au hasard". Si tu n'as pas d'idée 0 ou 1 sont les choix par défaut.
Après tu peux être plus malin, soit en regardant un graphique, soit en faisant un DL et résolvant l'équation linéaire.
Tu en prends un "au hasard". Si tu n'as pas d'idée 0 ou 1 sont les choix par défaut.
Après tu peux être plus malin, soit en regardant un graphique, soit en faisant un DL et résolvant l'équation linéaire.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
méthode de Newton
rubrique "algorithmes", et à la fin du doc (format pdf), la méthode est expliquée
avec majoration de la dérivée seconde.
ça demande de connaître la formule de Taylor
avec "reste intégral".
rubrique "algorithmes", et à la fin du doc (format pdf), la méthode est expliquée
avec majoration de la dérivée seconde.
ça demande de connaître la formule de Taylor
avec "reste intégral".
30 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
