La méthode de Newton-Raphson

[mathelot]

(uv)'=u'v+uv'

[feliraf]

je viens d'essayé votre dérivée pour calculé delta xi = F(x)/F'(x) , et sa marche pas je trouve pas le bon résultat

[feliraf]

La hauteur du niveau d’eau, h, augmente entre 0.5 heure et 3 heures (par rapport à un instant du temps choisi comme repère) selon la formule h = sin(0.5x) x^0.5. Evaluez, par la méthode de Newton, le moment (avec 4 chiffres exacts après la virgule) où l’eau atteint le niveau h = 1 m.

Moi j'ai fais pour trouve delta Xi = 1-sin(0.5x) x^0.5/-(cos(x*0.5)(x)^0.5+0.5(x)^-0.5*sin(x*0.5)) et aussi avec vôtre dérivée et sa marche pas non plus :/

[mathelot]

ça converge vers

vous avez changé d'équation entre temps ? il y avait un log
dans la 1ère égalité.

[feliraf]

oui je d'accord je l'ai fais avec la calculatrice mais avec la méthode ça marche et sa vient de mon delta Xi et je sais pas ou est mon problème

[feliraf]

non pas de log

[feliraf]

quand je dérive h -sin(0.5x) x^0.5=0 je retrouve toujours -(cos(x*0.5)(x)^0.5+0.5(x)^-0.5*sin(x*0.5))

[mathelot]

il manque un facteur 0.5 dans le 1er produit : u'v

et ensuite factoriser , dans la dérivée, par 0.5/Vx

[feliraf]

vous pouvez me donner le résultat , parce que j'ai refait et j'ai : ;)(0.5/x^0.5)sin(0.5x);)0.5x^0.5cos(0.5x)

[mathelot]

on note
Vx =
et



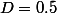
h(x)=sin(Dx)Vx


avec Leibniz :

h'(x)=Dcos(Dx)Vx+sin(Dx)D/Vx

en factorisant:

h'(x)=(D/Vx) (xcos(Dx)+sin(Dx))