Bonsoir !
Faire le soi-disant "changement de variables"
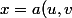,\;y=b(u,v))
c'est en fait "composer des fonctions" :
\mapsto f(a(u,v),b(u,v)),\;g=f\circ\Phi)
et la première relation à connaître est
=\dfrac{\partial f}{\partial x}(a(u,v),b(u,v))\dfrac{\partial a}{\partial u}(u,v)+\dfrac{\partial f}{\partial y}(a(u,v),b(u,v))\dfrac{\partial b}{\partial u}(u,v))
avec une notation contestable : dans
)
les lettres

n'ont pas le même statut. L'une (celle dans
)
) est une composante d'un couple de réels), l'autre (celle dans
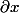
) est juste un numéro, celui de ce qui a été choisi comme première variable.
En prenant le temps (ce que je ne fais pas dans la suite) de noter les fonctions
\mapsto\dfrac{\partial f}{\partial x}(a(u,v),b(u,v)))
etc... on aurait une relation s'exprimant comme somme de deux produits de fonctions ce qui permet de dériver une deuxième fois.
Et on aurait :
+\dfrac{\partial}{\partial u}\Bigl(\dfrac{\partial f}{\partial y}\dfrac{\partial b}{\partial u}\Bigr))
+\dfrac{\partial}{\partial u}\Bigl(\dfrac{\partial f}{\partial y}\dfrac{\partial b}{\partial u}\Bigr)=\dfrac{\partial }{\partial u}\Bigl(\dfrac{\partial f}{\partial x}\Bigr)\dfrac{\partial a}{\partial u}+\dfrac{\partial f}{\partial x}\dfrac{\partial^2 a}{\partial u^2}+\dfrac{\partial }{\partial u}\Bigl(\dfrac{\partial f}{\partial y}\Bigr)\dfrac{\partial b}{\partial u}+\dfrac{\partial f}{\partial y}\dfrac{\partial^2 b}{\partial u^2})
puis en reprenant la formule du début en remplaçant

par
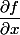
=\dfrac{\partial }{\partial x}\Bigl(\dfrac{\partial f}{\partial x}\Bigr)\dfrac{\partial a}{\partial u}+\dfrac{\partial }{\partial y}\Bigl(\dfrac{\partial f}{\partial x}\Bigr)\dfrac{\partial b}{\partial u}=\dfrac{\partial^2f}{\partial x^2}\dfrac{\partial a}{\partial u}+\dfrac{\partial^2f}{\partial y\partial x}\dfrac{\partial b}{\partial u})
et de même en reprenant la formule du début en remplaçant

par
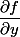
tu vois apparaître les dérivées doubles de

(comme tu le voudrais)
En revanche, pour ton changement de variables linéaire les dérivées secondes de

sont nulles.
En espérant ne pas avoir laissé d'erreurs, pas facile de taper du LaTex sur un éditeur de forum.
