Bonjour,
Comment déterminer l'équation de la droite de régression de y en x pour la série suivante, par la méthode des moindres carrés :
x 2 5 9 12 15 20 25 28
y 12 16 20 21 17 32 35 39
Et quel est le coefficient de corrélation linéaire?
Merci
Méthode des moindres carrés
4 messages
- Page 1 sur 1
bonsoir,
on dispose de 8 points de coordonnées)
l'indice i variant de 1 à 8.
l'idée n'est pas de trouver une droite minimisant
la (somme des) distance des points à celle-çi (une droite qui passerait au plus juste) car la distance d'un point à une droite est
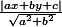
ie, une expression en a et b avec valeur absolue, donc pas
nécessairement dérivable.
On résoud donc un problème qui lui ressemble un peu, mais
qui lui, fait intervenir des fonctions dérivables !
on minimise la somme des "distances" verticales des points à la droite
de régression.
On suppose que cette droite de régression, inconnue, a une équation de la forme y=ax+b
on doit minimiser la somme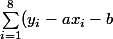^2)
parmi toutes les valeurs possibles pour a et b.
Remplace donc les) par leurs valeurs.
par leurs valeurs.
On obtient un trinome du second degré en a et b.
Annule la fonction dérivée relativement à , b fixé inconnu, puis la dérivée relativement à
, b fixé inconnu, puis la dérivée relativement à  (a fixé).
(a fixé).
on obtient un système 2x2 d'inconnues a et b.
remarque: il faut développer l'identité (a+b+c)^2
qui vaut)
on s'en aperçoit en posant d=b+c , en développant^2)
on dispose de 8 points de coordonnées
l'indice i variant de 1 à 8.
l'idée n'est pas de trouver une droite minimisant
la (somme des) distance des points à celle-çi (une droite qui passerait au plus juste) car la distance d'un point à une droite est
ie, une expression en a et b avec valeur absolue, donc pas
nécessairement dérivable.
On résoud donc un problème qui lui ressemble un peu, mais
qui lui, fait intervenir des fonctions dérivables !
on minimise la somme des "distances" verticales des points à la droite
de régression.
On suppose que cette droite de régression, inconnue, a une équation de la forme y=ax+b
on doit minimiser la somme
parmi toutes les valeurs possibles pour a et b.
Remplace donc les
On obtient un trinome du second degré en a et b.
Annule la fonction dérivée relativement à
on obtient un système 2x2 d'inconnues a et b.
remarque: il faut développer l'identité (a+b+c)^2
qui vaut
on s'en aperçoit en posant d=b+c , en développant
Bonjour,
excusez-moi de nuancer fortement l'affirmation de mathelot :
>
Mais si, on peut, si on le souhaite, trouver une droite minimisant la somme des distances des points à celle-çi. C'est un tout petit peu plus compliqué que de minimiser la somme des "distances verticales" ou celle des "distances horizontales" : C'est au choix du client !
On trouve les calculs respectifs à ces différents choix de régressions linéaires par moindres carrés dans tous les ouvrages "basiques" de statistiques.
Un résumé des formules correspondantes et donné au paragraphe 3 de l'article suivant :
http://www.scribd.com/people/documents/10794575-jjacquelin
Dans la liste, sélectionner l'article : Régressions coniques, quadriques. régressions linéaires et apparentées,...
( il ne s'agit pas de l'autre article : "Régressions et équations intégrales" qui s'applique à des cas plus compliqués)
excusez-moi de nuancer fortement l'affirmation de mathelot :
>
Mais si, on peut, si on le souhaite, trouver une droite minimisant la somme des distances des points à celle-çi. C'est un tout petit peu plus compliqué que de minimiser la somme des "distances verticales" ou celle des "distances horizontales" : C'est au choix du client !
On trouve les calculs respectifs à ces différents choix de régressions linéaires par moindres carrés dans tous les ouvrages "basiques" de statistiques.
Un résumé des formules correspondantes et donné au paragraphe 3 de l'article suivant :
http://www.scribd.com/people/documents/10794575-jjacquelin
Dans la liste, sélectionner l'article : Régressions coniques, quadriques. régressions linéaires et apparentées,...
( il ne s'agit pas de l'autre article : "Régressions et équations intégrales" qui s'applique à des cas plus compliqués)
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
