Méthode des éléments finis

[JeanJak]

Bonjour,

Je cherche à comprendre le principe général de la méthode des éléments finis (Finite-Element Method).

Dans mon cas, j'essaie de comprendre une application modélisant la température d'un corps selon cette méthode. Mes connaissances en Math étant assez limitées, je ne suis pas sûr de tout comprendre parfaitement. Dans ce cas thermique, je me demande comment cela fonctionne :

- Est-ce que chaque élément du maillage évolue selon les lois thermiques?
- Ou bien, est-ce le corps qui évolue globalement selon ces mêmes lois et nous pouvons y interpoler la température pour la déterminer au niveau d'une zone du corps choisie?

J'espère avoir été clair dans mes propos,
Merci d'avance,
JJ

[BQss]

Salut.
Comme ici tu es en dimension un il n'y a qu'une variable (la temperature),
tu discretises ton problème en modelisant la variation de temperature sur un axe. En ordonnées c'est les valeures de l'interpolée.

Tu divises ton maillage en N+1 intervalles de taille (sur lesquels on construit les elements finis), en placant N+2 points(generalement N+2 car il y a des conditions aux limites , c'est une question pratique).

Tu vas approcher maintenant ta solution par une fonction continue.
Un polynome par morceaux par exemple( le choix judicieux du degré depend de l'ordre de ton EDP, ici equa diff classique apparemment). Je sais pas laquelle tu as.

Pour simplifier prenons des fonctions affines sur chaque maillage tel que les f(xi) soient fixés(les degrés de liberté, ou on a posé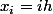 les sommets du maillaillage . Ansi on determine entierement la fonction affine par morceaux car deux points(ce sont les f(xi)) suffisent a determiner une fonction affine(sur chaque maillage) et donc la fonction affine par morceaux.
On verifie bien que les fonctions affines se recoupent continuement également.

On crée ensuite une base de fonction affines par morceaux(continue) pour cet espace de dimension N+2.
la base est definie de la sorte.
si i=j et 0 si non.
Ces fonctions sont affines et continues et forment une base de l'espace des fonctions affines par morceaux sur ce maillage.

Ainsi toute fonction de cet espace Vh s'ecrit:

f(x)=


Ensuite il faut ecrire ton probleme sous forme variationnelle(en dimension un avec des integrations par partie(on multiplie alors par une fonction v(x) adéquate tout en faisant attention aux conditions aux limites...) generalement on y arrive)).
Tu mets ainsi en evidence une forme bilineaire symetrique d'une part et une forme lineaire d'autre part(ces systemes admettent generalement des solutions "lax milgraam")

C'est là que tu remplaces la fonctions solution par ainsi que la fonction quelconque v(x) pour lesquelles l'égalité est réalisée.

Le systeme discret qui en découle admet bien une solution car la matrice est alors definie positive.
D'un point de vue topologique on peut egalement le prouver car Vh(l'espace discret) est inclu dans le hilbert sur lequel le probleme variationnelle continue est definie et comme il est fermé il est aussi complet et lax milgram s'applique.

Bref tu te retrouves avec un systeme lineaire(par linéarité il suffit de montrer que ca marche pour tout w(j) de la base, i.e que avec une matrice de taille N^2(ou N+2 selon les conditions aux limites):

Soit le système resultant


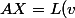A est la matrice des avec A la forme bilinéaire de la forme variationnelle définie plus haut.

L(v) le vecteur de taille N de coefficient avec L la forme linéaire définie plus haut

et X le vecteur solution dont les coefficient sont les

qu'on cherche.

Tu as alors trouvé la solution discrète f(x)= en trouvant les

Malheureusement si comme tu le dis tu n'as pas fait beaucoup de maths cela est compliqué a réaliser.

1)on passe sous forme variationnelle(c'est a partir de la qu'on va résoudre le probleme discret, a partir de l'equation d'origine la methode des elements finis ne s'applique pas, essaie plutot la methode des differences finies si non, qui est plus simple d'ailleurs. Pour cette seconde on discretise directement a partir d'aproximations d'operateurs differentiels directement depuis l'edp aux limites d'origine)
2)on cherche un espace adequate
3)on construit une base
4)on resoud le systeme discret judicieux qui correspond


Je te conseille donc d'etudier dans des bouquins le probleme car meme si le systeme est facile a resoudre par ordinateur au pire, ce qui est plus chiant c'est d'arriver jusqu'a la(si tu n'as pas beaucoup de notions mathematiques, meme si en dimension un c'est pas mal simplifié) alors que tu n'as que le probleme continue.



Voila tape dans google:
approximation des EDP
Methode des elements finis
Formulation variationnelle

Mais je te conseille plutot la methode des differences finies ou le passage a l'état discret ne pose pas de rélles complications..


Maintenant je suis désolé de ne plus pouvoir t'aider ou te répondre, j'ai un memoire a rendre pour dans 15 jours alors je te laisse avec ça, bonne chance!
Peut-être d'autres ici t'aideront.



PS:Je passe au passage un bonjour a Fahr , Yos, Sandrine et les autres. Salut les amis!

[JeanJak]

Merci pour ta réponse!!! Je vais regarder ça de plus près! Bon courage pour le mémoire!