Méthode de Cardan
34 messages
- Page 2 sur 2 - 1, 2
Re: Méthode de Cardan
Pour que tu comprennes les limites logiques de la méthode de Cardan , je résous complètement ton équation E(-6)9
Les racines cubiques de -8 , sont -2 , -2j , -2j^2 . Notons a l'une d'entre elles .
Les racines cubiques de -1 sont -1 , -j , -j^2 . Notons b l'une d'entre elles .
On a toujours a^3 b^3 = -p^3/27 , mais certainement pas ab=-p/3 .
On a seulement les paires {-2 ,-1} , {-2j,-j^2} , et {-2j^2,-j} qui donnent les trois racines -3 , -2j-j^2=1-j , et -2j^2-j=2+j
Les racines cubiques de -8 , sont -2 , -2j , -2j^2 . Notons a l'une d'entre elles .
Les racines cubiques de -1 sont -1 , -j , -j^2 . Notons b l'une d'entre elles .
On a toujours a^3 b^3 = -p^3/27 , mais certainement pas ab=-p/3 .
On a seulement les paires {-2 ,-1} , {-2j,-j^2} , et {-2j^2,-j} qui donnent les trois racines -3 , -2j-j^2=1-j , et -2j^2-j=2+j
Re: Méthode de Cardan
tournesol a écrit:Mehdi , ton exo n'est pas aussi ambitieux que tu semble le croire .
On ne te demande surtout pas de résoudre toute équation du type Epq .
Dans la première question , tu as montré que
(u^3+v^3=-q et 3uv=-p) implique (u+v est racine de Epq) (1)
Dans la deuxième question , on te donne une méthode pour esperer trouver u et v , et je dis bien espérer , car tu n'auras que u^3 et v^3 , obtenus avec la condition u^3 v^3 =-p^3/27 .
Par chance , la fonction cube étant bijective sur R , cette condition est equivalente sur R à 3uv=-p .
C'est pour cela que le delta de ton équation du second degré t'a été donné positif (egal à 49) .
Ton exo n'a que des objectis simples .
tu calcules U^3 et v^3 , tu obtiens -8 et -1 dont les racines cubiques réeles sont -2 et -1 .
On a bien 3uv =6 . Donc d'après (1) , u+v=-3 est racine de E(-6)9 .
Le détail qui me tracasse est : a-t-on équivalence ? Ou après avoir résolu l'équation du seconde degré il faut encore vérifier que :
Re: Méthode de Cardan
@Tournesol.
Mon exercice s'intéresse qu'aux solutions réelles et dans un exercice précédent on a démontré que en posant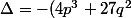) :
:
Si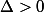 alors l'équation
alors l'équation  possède 3 racines réelles.
possède 3 racines réelles.
Si alors l'équation
alors l'équation  possède 1 racines réelle.
possède 1 racines réelle.
Si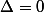 : si
: si 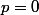 on a une unique solution qui est
on a une unique solution qui est  et si
et si 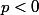 on a 2 racines.
on a 2 racines.
En revenant à notre exercice, la dernière question que j'ai résolu est :
Dans le cas où donner la seule racine réelle de
donner la seule racine réelle de 
J'ai fait :
Calculons les racines de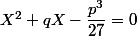
Son déterminant vaut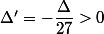
Cette équation possède 2 racines réelles qui sont :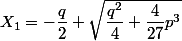 et
et 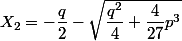
L'unique racine de est donnée par :
est donnée par :
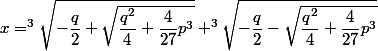
Mon exercice s'intéresse qu'aux solutions réelles et dans un exercice précédent on a démontré que en posant
Si
Si
Si
En revenant à notre exercice, la dernière question que j'ai résolu est :
Dans le cas où
J'ai fait :
Calculons les racines de
Son déterminant vaut
Cette équation possède 2 racines réelles qui sont :
L'unique racine de
Re: Méthode de Cardan
D'accord avec toi pour ton dernier message .
Pour l'avant dernier , tu as bien vu qu'on n'a pas equivalence puisque sur 9 produits calculés , seuls 3 verifiaient la conditition 3uv=-p . L'autre conditiln est vérifiée pusque u^3 et v^3 sont les racines de ...
Felicitations Mehdi ; tu essaie de comprendre et tu ne laches rien .
Pour l'avant dernier , tu as bien vu qu'on n'a pas equivalence puisque sur 9 produits calculés , seuls 3 verifiaient la conditition 3uv=-p . L'autre conditiln est vérifiée pusque u^3 et v^3 sont les racines de ...
Felicitations Mehdi ; tu essaie de comprendre et tu ne laches rien .
Re: Méthode de Cardan
Alors pourquoi il est écrit dans mon livre la remarque suivante :
Comme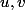 sont supposés réels, la relation
sont supposés réels, la relation 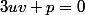 est équivalente à :
est équivalente à : 
Comment on sait que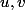 sont supposés réels
sont supposés réels 
Comme
Comment on sait que

Re: Méthode de Cardan
Un nombre réel (non nul) admet 3 racines cubiques dont une seule est réelle.!!
Re: Méthode de Cardan
La fonction cube est une bijection de R sur R , donc elle est injective ie deux reels qui ont la même image sont égaux.
Donc deux reels qui ont le même cube sont égaux .
Or les réels uv et ont le même cube , donc ils sont égaux.
ont le même cube , donc ils sont égaux.
La réciproque est évidente: deux nombres égaux ont le même cube .
Donc deux reels qui ont le même cube sont égaux .
Or les réels uv et
La réciproque est évidente: deux nombres égaux ont le même cube .
Re: Méthode de Cardan
Oui j'ai compris je suis d'accord on sait qu'il existe des solutions réelles donc x est un réel. Mais qui nous dit que u et v sont réels ? On a x=u+v. On peut avoir u et v complexes et x réel non ?
Le point bloquant est : comment on sait que u et v sont des réels ?
Le point bloquant est : comment on sait que u et v sont des réels ?
Re: Méthode de Cardan
Il n'y a pas de point bloquant. En effet qui a dit que u et v sont réels?
Une équation du second n'a pas forcément des racines réelles, à ma connaissance.
Une équation du second n'a pas forcément des racines réelles, à ma connaissance.
Re: Méthode de Cardan
Après même si y a pas équivalence c'est pas grave suffit de vérifier que la solution de l'équation du second degré vérifie bien les 2 conditions. Puis ici l'exo se restreint aux solutions réelles.
Mathelot comment savez vous que u et v sont pris conjugués ?
Mathelot comment savez vous que u et v sont pris conjugués ?
Re: Méthode de Cardan
mehdi-128 a écrit:Calculons les racines de
Son déterminant vaut
Cette équation possède 2 racines réelles qui sont :et
L'unique racine deest donnée par :
ces formules sont fausses...si on rentre le dénominateur 2 dans la racine carrée, il n'y a plus de facteur 4 devant p^3:
les formules exactes sont:
Cette équation possède 2 racines réelles qui sont :
L'unique racine de
Modifié en dernier par mathelot le 11 Mar 2019, 19:16, modifié 1 fois.
Re: Méthode de Cardan
Mehdi, aurais-tu le courage de répercuter la modif sur les quelques formules de racines cubiques, il s'agit de remplacer le 4 devant p^3 par 1...merci d'avance
34 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
