Méthode de Cardan
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 05 Mar 2019, 18:39
par mehdi-128 » 05 Mar 2019, 18:39
Bonsoir,
Soient

et

des réels. On s'intéresse à l'équation
)
suivante :
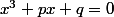
1/ La méthode de Cardan consiste à trouver 2 nombres

et

tels que
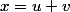
soit une racine de

a/ Montrer qu'il suffit d'avoir

et
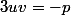
J'ai réussi cette question :
^3 + p(u+v) +q = v^3 +u^3+ (3uv)v + (3uv)u +pu+pv+q)
D'où :
^3 + p(u+v) +q = -q + -pv - pu + pu +pv +q =0)
b/ Vérifier que
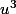
et
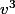
sont alors racines d'une équation d'une second degré qu'on précisera.
Pas compris cette question

-
mathelot
 par mathelot » 05 Mar 2019, 18:45
par mathelot » 05 Mar 2019, 18:45
bonsoir,
soient deux réels x et y
On suppose connus leur somme S et leur produit P
x et y sont les solutions de l'équation d'inconnue X:
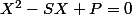
preuve:
x et y sont solutions de l'équation
(X-y)=0)
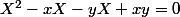
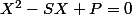
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 05 Mar 2019, 19:01
par mehdi-128 » 05 Mar 2019, 19:01
Je n'ai rien compris.
-
aviateur
 par aviateur » 05 Mar 2019, 19:15
par aviateur » 05 Mar 2019, 19:15
Si tu connais

et 3 uv donc aussi uv et donc

En posant X=u^3 et
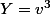
, tu connais donc S=X+Y et P=XY donc tu peux les calculer en résolvant une équation de degré 2.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 05 Mar 2019, 20:58
par mehdi-128 » 05 Mar 2019, 20:58
Montrons que
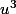
et
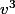
sont solutions de
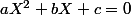
avec
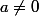
D'après le cours

et

sont racines de cette équation si et seulement si :
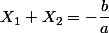
et
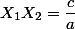
En utilisant votre indication Aviateur, posons :

et

On a :
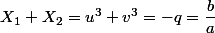
Et :
^3 = -\dfrac{p^3}{27} = \dfrac{c}{a})
Mais je vois pas comment trouver

On a 2 équations et 3 inconnues

-
aviateur
 par aviateur » 05 Mar 2019, 21:25
par aviateur » 05 Mar 2019, 21:25
mais a=1. !!!!!!!!!!!!!!!!!!!!!
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 05 Mar 2019, 21:38
par mehdi-128 » 05 Mar 2019, 21:38
Comment savez-vous que a=1 ? C'est le détail qui m'échappe...
-
aviateur
 par aviateur » 05 Mar 2019, 21:47
par aviateur » 05 Mar 2019, 21:47
Ton equation tu l'a prends à un facteur près autant prendre a=1
et puis @mathelot t'a donné l'équation!
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 05 Mar 2019, 21:59
par mehdi-128 » 05 Mar 2019, 21:59
Sinon cela vient du fait que si on pose :

et
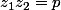
alors
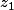
et
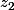
sont racines de :
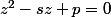
Je trouve l'équation :
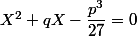
(E)
Par contre un détail m'interpelle :
Il faut montrer que :
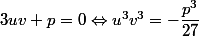
Donc il faut montrer que

sont des réels mais je vois pas comment faire

Car la suite est :
Trouver la solution réelle de 
Pour cela il faudrait montrer que :
(
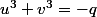
et
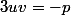
)

(

et

sont racines de (E) )
-
aviateur
 par aviateur » 05 Mar 2019, 22:13
par aviateur » 05 Mar 2019, 22:13
Je crois que tu n'as pas compris. C'est pas u et v racines de E mais u+v racine de E
Avec ton exemple
x^3 - 6x +9=0 il faut u^3+v^3=-9 et 3u v= 6 , i;e u v =6 mais c'est u+v qui est racine.
Donc ici il faut prendre v=2/u. Ce qui donne u^3+8/u^3=-9.
Tu as ton équation de degré 2 qui te donne u^3, puis u,v et donc u+v.
Modifié en dernier par aviateur le 05 Mar 2019, 22:37, modifié 1 fois.
-
mathelot
 par mathelot » 05 Mar 2019, 22:33
par mathelot » 05 Mar 2019, 22:33
mehdi-128 a écrit:Je n'ai rien compris.
On calcule la somme
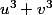
et le produit
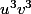
Ce qui conduit à une équation du second degré d'inconnues
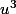
et

Ensuite on doit se débrouiller pour calculer u et v.
Une solution de l'équation de degré 3 est u+v.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 05 Mar 2019, 22:49
par mehdi-128 » 05 Mar 2019, 22:49
Je vois la méthode. Mais je n'ai pas compris c'est où qu'on a montré l'implication suivante :
(
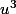
et
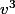
sont alors racines d'une équation d'une second degré )

(
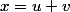
est racine de

)
-
aviateur
 par aviateur » 05 Mar 2019, 22:54
par aviateur » 05 Mar 2019, 22:54
Il faut prendre les choses dans l'ordre qui t'es donné:
On pose x=u+v telle que f(x)=f(u+v)=0. Si u^3+ v^3 =-q et 3uv=-p. La question 1) montre que u+v est racine de E.
Il faut donc chercher (u,v) tel que u^3+ v^3 =-q et 3uv=-p. Mais cela revient à résoudre une équation de degré 2 de la Forme X^2-SX+P=0
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 05 Mar 2019, 23:02
par mehdi-128 » 05 Mar 2019, 23:02
Pour le calcul je trouve :
En posant
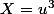
on a :
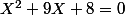
Ou encore :
^2 - \dfrac{49}{4} = 0)
Soit :
(X + \dfrac{9}{2} + \dfrac{7}{2})=0)
Donc :
(X + 8)=0)
L'équation admet 2 solutions qui sont

Donc
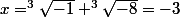
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 05 Mar 2019, 23:28
par mehdi-128 » 05 Mar 2019, 23:28
aviateur a écrit:Il faut prendre les choses dans l'ordre qui t'es donné:
On pose x=u+v telle que f(x)=f(u+v)=0. Si u^3+ v^3 =-q et 3uv=-p. La question 1) montre que u+v est racine de E.
Il faut donc chercher (u,v) tel que u^3+ v^3 =-q et 3uv=-p. Mais cela revient à résoudre une équation de degré 2 de la Forme X^2-SX+P=0
Ah d'accord.
"Cela revient" signifie qu'il y a équivalence ? D'où provient cette équivalence ? Du cours ?
Dans mon cours il est écrit :
Soit
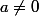

et

sont racines de
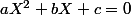
si et seulement si :
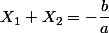
et
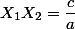
-
aviateur
 par aviateur » 06 Mar 2019, 00:01
par aviateur » 06 Mar 2019, 00:01
mehdi-128 a écrit:Ah d'accord.
"Cela revient" signifie qu'il y a équivalence ? D'où provient cette équivalence ? Du cours ?




Encore un dérapage.
Il y a équivalence entre quoi et quoi?
D'ailleurs quand je dis "cela revient.....blabla" c'est une circonlocution qu'il faut comprendre à bon escient.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 06 Mar 2019, 00:09
par mehdi-128 » 06 Mar 2019, 00:09
Dans la question 1 on a montré l'implication :
(

et
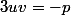
)

(
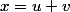
est une racine de

)
Dans la question 2 on a montré que :
(

et
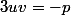
)

(
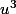
et
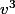
sont solutions d'une équation de degré 2)
Ou bien pour la question 2 il y a équivalence ?
Car pour la question 3 j'ai besoin de l'implication suivante :
(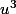 et
et 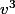 sont solutions d'une équation de degré 2)
sont solutions d'une équation de degré 2)  (
(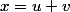 est une racine de
est une racine de  )
)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 06 Mar 2019, 00:39
par mehdi-128 » 06 Mar 2019, 00:39
Car mon livre écrit pour la question 2 :
Comme
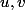
sont supposés réels (en fait on l'a démontré dans l'exercice précédent) la relation
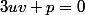
est équivalente à :

Il suffit alors que :
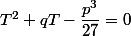
Pas compris pourquoi on doit justifier qu'il y a équivalence ici

-
aviateur
 par aviateur » 06 Mar 2019, 06:38
par aviateur » 06 Mar 2019, 06:38
Tu as le don de tout déformer ou quoi ?
Est solution d'une equation ça veut pas dire n'importe qu elle équation.
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 06 Mar 2019, 08:34
par tournesol » 06 Mar 2019, 08:34
Mehdi , ton exo n'est pas aussi ambitieux que tu semble le croire .
On ne te demande surtout pas de résoudre toute équation du type Epq .
Dans la première question , tu as montré que
(u^3+v^3=-q et 3uv=-p) implique (u+v est racine de Epq) (1)
Dans la deuxième question , on te donne une méthode pour esperer trouver u et v , et je dis bien espérer , car tu n'auras que u^3 et v^3 , obtenus avec la condition u^3 v^3 =-p^3/27 .
Par chance , la fonction cube étant bijective sur R , cette condition est equivalente sur R à 3uv=-p .
C'est pour cela que le delta de ton équation du second degré t'a été donné positif (egal à 49) .
Ton exo n'a que des objectis simples .
tu calcules U^3 et v^3 , tu obtiens -8 et -1 dont les racines cubiques réeles sont -2 et -1 .
On a bien 3uv =6 . Donc d'après (1) , u+v=-3 est racine de E(-6)9 .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités



