Bonjour,
je suis en 3ème année de licence de maths. J'ai un petit exercice sur les mesures que je ne sais pas trop par quel bout prendre. Si vous pouviez me guider et m'éclairer :
"montrer que toute fonction qui est égale presque partout à une fonction mesurable est mesurable."
Merci d'avance
Mesures
6 messages
- Page 1 sur 1
Hello,
C'est typiquement le genre d'exos qui m'embête aussi en ce moment... Et je suppose que la rédaction risque d'être ardue !
Déjà, pour te donner une idée du boulot à accomplir: prends une fonction f : [0,1] -> R, continue donc mesurable. Et maintenant, prends g qui "presque la même" : g = f sur ]0,1], et g discontinue en 0. Et essaie de montrer que g est mesurable : c'est déjà pas de la tarte !
De manière générale, considère par exemple une fonction mesurable f, et l'ensemble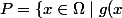 \neq f(x) \right\}) . P est de mesure nulle. Après, j'vois pas encore vraiment quoi en faire.
. P est de mesure nulle. Après, j'vois pas encore vraiment quoi en faire.
Dans l'absolu, faudrait montrer que pour tout borélien B' de la tribu d'arrivée, \in \mathcal{A}) , la tribu de départ.
, la tribu de départ.
Pour cela, peut-être faut-il étudier les intersections (ou en tout cas les points en commun) de B' et P ?..
C'est typiquement le genre d'exos qui m'embête aussi en ce moment... Et je suppose que la rédaction risque d'être ardue !
Déjà, pour te donner une idée du boulot à accomplir: prends une fonction f : [0,1] -> R, continue donc mesurable. Et maintenant, prends g qui "presque la même" : g = f sur ]0,1], et g discontinue en 0. Et essaie de montrer que g est mesurable : c'est déjà pas de la tarte !
De manière générale, considère par exemple une fonction mesurable f, et l'ensemble
Dans l'absolu, faudrait montrer que pour tout borélien B' de la tribu d'arrivée,
Pour cela, peut-être faut-il étudier les intersections (ou en tout cas les points en commun) de B' et P ?..
Ca marche ça ? :
f = g + h avec g mesurable et h nul en dehors d'un ensemble de mesure nulle.
Il sufft de montrer que h est mesurable.
h^{-1}(n'importe quoi) sera contenu dans un {0} U ensemble contenu dans ensemble de mesure nulle donc mesurable (j'imagine qu'on bosse avec la mesure de Lebesgue oeuf corse)
f = g + h avec g mesurable et h nul en dehors d'un ensemble de mesure nulle.
Il sufft de montrer que h est mesurable.
h^{-1}(n'importe quoi) sera contenu dans un {0} U ensemble contenu dans ensemble de mesure nulle donc mesurable (j'imagine qu'on bosse avec la mesure de Lebesgue oeuf corse)
bjr,
le problème équivaut à:
Soit X un ensemble, inclu dans un ensemble Y mesurable et de mesure nulle.
X est-il mesurable ? évidemment, on peut toujours poser=0) dans ce cas.
dans ce cas.
içi
Dans le cas inverse, s'il existe de tels ensembles X, la fonction caractéristique coïncide presque partout avec la fonction nulle mais n'est pas mesurable.
coïncide presque partout avec la fonction nulle mais n'est pas mesurable.
ceçi dit, il semble que la mesure de Lebesgue est complète, on la définit sur une tribu où l'on adjoint aux boréliens les ensembles négligeables.
le problème équivaut à:
Soit X un ensemble, inclu dans un ensemble Y mesurable et de mesure nulle.
X est-il mesurable ? évidemment, on peut toujours poser
içi
Dans le cas inverse, s'il existe de tels ensembles X, la fonction caractéristique
ceçi dit, il semble que la mesure de Lebesgue est complète, on la définit sur une tribu où l'on adjoint aux boréliens les ensembles négligeables.
Salut,
Ca n'a pas de sens de parler de mesure d'une partie négligeable si la partie n'est pas mesurable.. Ici rien nous dit qu'il travaille avec la mesure de Lebesgue qui ne s'applique que sur (souvent pour n=1) si je ne m'abuse .
(souvent pour n=1) si je ne m'abuse .
Il doit te manquer une hypothèse du genre si \longrightarrow (\Omega)) et
et  \longrightarrow (\Omega)) où
où  est muni d'une tribu quelconque. Et si
est muni d'une tribu quelconque. Et si 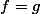
 et
et  est
est 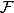 -mesurable alors on peut montrer facilement que
-mesurable alors on peut montrer facilement que  est
est  -mesurable si
-mesurable si  est la tribu complétée de
est la tribu complétée de 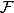 (on a rajouté les négligeables) :
(on a rajouté les négligeables) :
Soient=g(x)\}; B \in \Omega) . On a alors
. On a alors
=(f^{-1}(B) \cap A) \cup (f^{-1}(B) \cap A^{c}))
 \cup (f^{-1}(B) \cap A^{c}))
Or \in \mathcal{F}) donc dans
donc dans  et
et  \cap A^{c}) \sub A^{c}) qui est de mesure nulle par hypothèse donc négligeable donc dans
qui est de mesure nulle par hypothèse donc négligeable donc dans  d'où
d'où  \in \mathcal{E})
Ca n'a pas de sens de parler de mesure d'une partie négligeable si la partie n'est pas mesurable.. Ici rien nous dit qu'il travaille avec la mesure de Lebesgue qui ne s'applique que sur
Il doit te manquer une hypothèse du genre si
Soient
Or
Dyo a écrit:Salut,
Ca n'a pas de sens de parler de mesure d'une partie négligeable si la partie n'est pas mesurable..
Il s'agit dans les deux cas de compléter une mesure. pour moi, certains ensembles négligeables ne sont pas mesurables (on ne les obtient pas comme une suite finie d'intersections et de réunions dénombrables disons de boréliens) mais ils sont mesurés (de mesure nulle). :zen:
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
