Mesure d'irrationnalité de pi
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
par busard_des_roseaux » 01 Oct 2007, 22:49
Bonjour,
J'ai besoin d'un peu d'aide à la question 3.
merçi d'avance.
Exercice: Mesure d'irrationalité de
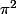
et
Soit
= \sum_{n=1}^{+\infty} \, \frac{1}{n^2}= \frac{\pi^2}{6})
.
Q.1:
Pour
 \in N^{2})
, on pose
.
Prouver que
-\sum_{k=1}^{r} \, \frac{1}{k^2})
et que
)
si
.
Q.2:
soit
=\frac{1}{n!} \, \frac{d^{n}}{dx^{n}} \, \left( x^n {(1-x)}^n \right))
le n-ième polynôme de Legendre. Prouvez que
.
Q.3:
On pose:
 {\left( 1-y \right)}^{n}}{1-xy} \, dxdy)
.
Démonter que
+ \, a_{n})
avec
.
On note
=PPCM(1,2,\cdots,n))
. Vérifiez que
]}^2 \,b_{n})
et
]}^2 \,a_{n})
sont entiers.
Q.4:
En utilisant l'encadrement:
 \leq 3^{n})
, montrer que
}^{n})
.
Q.5:
Prouvez que
}^n \int_{0}^{1}\int_{0}^{1} \, \frac{x^{n} y^{n} {\left( 1-x \right)}^{n}{\left( 1-y \right)}^{n}}{{\left( 1-xy \right)}^{n+1}} \, dxdy)
.
Q.6:
Montrer que
(1-y) \leq {\left( 1 - \sqrt{xy} \right)}^{2})
pour tout
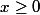
, pour tout
.
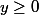
En déduire que:
 }^{5n} \leq 1.65 \times {\left( 0.0902 \right)}^{n})
.
Q.7:
En remarquant que:
}^{n}{\left( 1-y \right)}^{n}}{{\left( 1-xy \right)}^{n+1}} \, dxdy)
pour
montrer que:
}^{n}.)
par busard_des_roseaux » 02 Oct 2007, 17:16
Q 1.
On développe en série. Comment montre t on que l'on peut permutter
série et intégrale. convergence croissante ?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
par fahr451 » 02 Oct 2007, 19:09
oui
convergence monotone
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 89 invités
