On désigne pas

la mesure de Lebesgue sur
))
et par
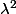
la mesure de Lebesgue sur
))
.
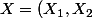)
est un couple aléatoire défini sur un espace probabilisé
)
, de loi de probabilité

,

est l'application symétrie dans

:
=(x_2,x_1))
et
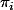
avec
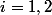
est la projection
 \to x_i)
.
1. Montrer que

est mesurable et que
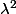
est invariante par

(i.e. la mesure image de
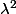
par

est
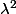
)
2. On suppose que

est invariante par

(i.e. la mesure image de

par

est

). Montrer que :
2.a. les marginales
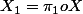
et
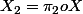
ont même loi de probabilité ;
2.b. si

admet une densité
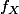
par rapport à
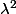
, alors
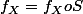
presque partout
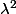
.
3. Soit h l'application de

dans

définie par :
 = (inf(x_1,x_2),sup(x_1,x_2)))
.
3.a. Montrer que
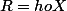
est un couple aléatoire.
3.b. Soient
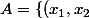 \in \mathbb{R}^2 | x_1 \leq x_2 \})
et
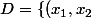 \in \mathbb{R}^2 | x_1 = x_2 \})
. Vérifier que

et

sont des parties boréliennes de

et montrer que pour tout
)
on a :
 = P_X(B \cap A) + P_X(S^{-1}(B \cap A)) - P_X(B \cap D))
,
(1) où
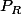
désigne la loi de probabilité de

.
3.c. Démontrer à l'aide de
(1) que :
3.c.i. si

est invariante par

,
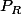
admet par rapport à

la densité
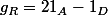
;
3.c.ii. si

admet la densité
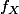
par rapport à
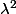
,
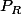
admet la densité
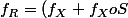1_A)
par rapport à
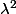
.
Passons à la partie réponse, je suis qu'au début de l'exercice mais j'essaie de comprendre chaque question :p
1. On sait que

est linéaire en dimension finie, donc

est continue, ce qui implique que S est mesurable.
Ensuite je voulais montrer que
)
on a
) = \lambda^2(B))
, je voulais du coup utiliser la théorème de l'unicité des mesures, mais ça me pose problème pour l'appliquer.
2.a. J'ai pas compris dans mon cours le principe des lois marginales, du coup je comprends pas comment le prouver.
2.b. Je pensais partir du fait

admet une densité
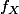
par rapport à

donc en fait calculer
)=\int_{\mathbb{R}^2} 1_{S^{-1}(B)} f_X d\lambda^2)
