Mesure absolument continue par rapport à une autre

[Dyo]

Bonjour,

J'aimerais savoir si un résultat est vrai (je ne le trouve nulle part, c'est certainement faux mais je n'en suis pas sûr, et si c'était vrai ça m'arrangerait grandement =) ) :

Si P est une mesure à densité sur par rapport à une mesure de référence (qui n'intervient pas ici) et Q une probabilité absolument continue par rapport à P admettant pour dérivée de Radon Nikodym .

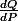
Bon déjà Q aussi une densité disons par rapport à .
On a la relation .

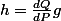
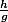
Le truc c'est que est positive mais pas nécessairement strictement. Or on a besoin de considérer le quotient . Pour palier à ça on peut poser qui est une densité strictement postivite et on peut ainsi considérer le quotient.

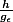
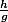
En fait j'aimerais savoir si dire que " tend vers quand tend vers 0" est envisageable même si le dénominateur de la limite peut s'annuler. Mais s'il s'annule c'est que h s'annule aussi (et "plus vite" peut être) et donc est-ce qu'il est juste de dire :
tend vers si et vers 0 sinon. (quand tend vers 0).

Merci d'avance, si quelqu'un peut un petit peu m'éclairer

[Doraki]

Pourquoi tu essayes de diviser h par g alors que tu sais DEJA que h = (dQ/dP) * g ?

Si g s'annule quelquepart alors h y sera automatiquement nulle elle aussi, et la valeur de dQ/dP à cet endroit là n'a absolument aucune signification.

(h/g) n'est jamais définie quand g s'annule, mais peut-être qu'elle est prolongeable (par exemple si h = g), et peut-être que non (par exemple si h = sqrt(g))

Et puis quant à h/gepsilon, ben il est toujours nul aux endroits qui t'embêtent donc en fait tu veux dire que h/g = lim de 0/e = 0 ?

[Dyo]

Si g s'annule quelquepart alors h y sera automatiquement nulle elle aussi, et la valeur de dQ/dP à cet endroit là n'a absolument aucune signification.

Oui ça d'accord.

(h/g) n'est jamais définie quand g s'annule, mais peut-être qu'elle est prolongeable (par exemple si h = g), et peut-être que non (par exemple si h = sqrt(g))

Ok du coup y'a un soucis.

En fait j'ai une inégalité démontrée dans le cas où g est strictement positive et qui fait intervenir h/g.
Et "apparemment" il est possible de généraliser le résultat dans le cas où g est positive en considérant le que j'ai défini au dessus et en faisant tendre dans le résultat le quotient vers , donc tu me dis que ça n'a pas de sens ? Du coup la généralisation ne s'effectue pas comme ça ?

[Doraki]

Ben à moins que ce soit plus compliqué que ce que je comprends dans ce que tu dis ou que je me trompe, h/ge = 0 là où g s'annule donc juste prendre la limite de ça en faisant tendre epsilon vers 0 ça m'a l'air de servir à rien.

Enfin intuitivement, je serais plus prompt à regarder le comportement de h/g autour du point critique que de regarder 0/gepsilon = 0 sur le point critique.
Ptetre qu'il faut regarder h/gepsilon autour du point critique mais je vois pas ce que ça apporte par rapport à simplement h/g.

[Dyo]

Oui je vois .. en plus g peut etre nulle sur un ensemble infini indénombrable (bref une partie quelconque de R)... En fait ça me gène pas que le quotient h/g_epsilon soit nul , la formule reste bonne.

Bon bah je vais réfléchir à autre chose. Merci en tout cas.