Message suprimé

par **Math_sup** » 29 Déc 2012, 12:15

.... :doh: :hum: :bad: :mur: :cry: :triste: :dodo: .........

par **lionel52** » 29 Déc 2012, 12:49

mmmh c'est faux quand même, tu as aucune condition sur g en l'infini, tu prends g(t) = x(x-1)

x(t) =x³/6 - x²/2 + 0.1 ça marche pas..

par **Math_sup** » 29 Déc 2012, 13:48

lexemple que tu as donner ne convient pas puisque x(t) doit être entre 0 et 1

par **chelsea-asm** » 29 Déc 2012, 13:53

Math_sup a écrit:lexemple que tu as donner ne convient pas puisque x(t) doit être entre 0 et 1

Son exemple marcherait pour x=3
27/6 - 9/2 + 0,1 = 0,1

par **Math_sup** » 29 Déc 2012, 14:08

chelsea-asm a écrit:Son exemple marcherait pour x=3
27/6 - 9/2 + 0,1 = 0,1

mais la condition initiale est entre 0 et 1 , et on vois que x est décroissante

par **Math_sup** » 29 Déc 2012, 16:01

pas d'idées ?

par **lionel52** » 29 Déc 2012, 16:15

Ecoute pour T = 17 mon exemple fonctionne et vu que t'as donné aucune précision nulle part

par **Math_sup** » 29 Déc 2012, 16:37

Voila l'exo :
Soit g une fonction de R dans R ,de classe

, telle que

pour tout

.
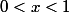
soit

et soit x une solution sur [0,T[ du problème

.
Montrer que 0<x(t)<1 pour tout t \in [o,T[ :++:
En déduire que le problème

admet une solution globale unique sur

:++:
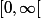
Montrer que cette solution vérifie

:--:

par **lionel52** » 29 Déc 2012, 18:57

C'est mieux comme ça en mettant les questions exactes ah ah :marteau:

cependant tu ne sais rien sur g après 1 donc ça va être difficile

par **Math_sup** » 30 Déc 2012, 09:20

on a x'=g(x)
x est décroissante donc

pour tout

x est minoré donc admet une limite !
faut prouver que cette limite = 0
quelqu'un a une idée ?
s'il vous plait