Matrices
80 messages
- Page 2 sur 4 - 1, 2, 3, 4
par kazeriahm » 16 Mar 2009, 17:51
bon pour revenir à ton problème :
la formule du binome de Newton ne s'utilise que si a et b commutent. Vérifie le dans ton cas (identifie bien qui sont a et b, ne dis pas I3=3I comme plus haut, ca n'a pas de sens). Après, intéresse toi aux puissances de B. Calcule B^2, B^3, B^4... juste pour voir.
la formule du binome de Newton ne s'utilise que si a et b commutent. Vérifie le dans ton cas (identifie bien qui sont a et b, ne dis pas I3=3I comme plus haut, ca n'a pas de sens). Après, intéresse toi aux puissances de B. Calcule B^2, B^3, B^4... juste pour voir.
par kazeriahm » 16 Mar 2009, 23:17
et donc ? quelles sont tes impressions remarques critiques suggestions sentiments idées ? tu attends les bras croisés ?
par juju78 » 17 Mar 2009, 00:05
ben a partir de B^3 on a une matrice nulle
mais je ne vois pas quoi conclure par rapport à la formule précedente
mais je ne vois pas quoi conclure par rapport à la formule précedente
par Joker62 » 17 Mar 2009, 00:10
A partir du rang 3 on a une matrice nulle.
Et tu vois pas le rapport avec la formule précédente ?
Ecris la forme développée si tu vois rien...
Et tu vois pas le rapport avec la formule précédente ?
Ecris la forme développée si tu vois rien...
par juju78 » 17 Mar 2009, 11:32
dsl si j'ai du mal mais c'est la premiere fois que je fais un exo de ce type, on en a pas encore fait en cours
On a donc une matrice nulle a partir du rang 3
donc on prend n =3 ?
On a donc une matrice nulle a partir du rang 3
donc on prend n =3 ?
par fatal_error » 17 Mar 2009, 12:11
La question initiale : calculer A^n pour tout n
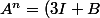^n)
Que vaut A^n?
Es-tu convaincu de ta réponse?
kazeriahm t'as conseillé de calculer les premieres puissances de B pour voir ce qu'il se passait.
Si tu n'as toujours pas d'idées, tu peux maintenant essayer de calculer les premieres puissances de A.
Si tu ne sais pas comment, tu peux relire les posts précédents...
Que vaut A^n?
on prend n =3
Es-tu convaincu de ta réponse?
kazeriahm t'as conseillé de calculer les premieres puissances de B pour voir ce qu'il se passait.
Si tu n'as toujours pas d'idées, tu peux maintenant essayer de calculer les premieres puissances de A.
Si tu ne sais pas comment, tu peux relire les posts précédents...
la vie est une fête 
par juju78 » 17 Mar 2009, 12:37
On a
etc..
A ne devient jamais une matrice nulle, quelque soit n
Sinon pour B, ca veut dire que a partir de k = 3 alors A= 0 ?
etc..
A ne devient jamais une matrice nulle, quelque soit n
Sinon pour B, ca veut dire que a partir de k = 3 alors A= 0 ?
par fatal_error » 17 Mar 2009, 12:43
etc..
Et si tu allais un peu plus loin? Par ailleurs, on ne peut pas savoir si tu utilises la formule du binome ou si tu developpes 3I+B = C pour elever C a la puissance n.
Sinon pour B, ca veut dire que a partir de k = 3 alors A= 0 ?
pas compris.
la vie est une fête
par SimonB » 17 Mar 2009, 12:59
Il faudrait sérieusement revoir les cours de logique et de raisonnement mathématiques, histoire d'arrêter d'écrire des trucs qui n'ont aucun sens.
Entre autres exemples : on te demande de calculer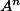
pour n un entier, tu ne PEUX donc pas "prendre n=3", n est donné par l'énoncé, bien que quelconque. Le "à partir de k=3 A=0" montre une autre sérieuse erreur de compréhension : A est donnée par l'énoncé également et ne dépend pas de k.
Bref, avant de s'avancer sur le cours, revoir les bases !
Entre autres exemples : on te demande de calculer
Bref, avant de s'avancer sur le cours, revoir les bases !
par kazeriahm » 17 Mar 2009, 19:49
A=3I+B
La formule de Newton te dit que si a et b commutent, alors
(a+b)^n=somme( bla bla bla)
Ici, ton problème est de calculer A^n, et tu sais que quand k>=3, B^k=0.
Voilà tout ce que tu as besoin d'avoir en tête. Il n'y a plus que deux lignes avant que tu puisses donner une expression de A^n
La formule de Newton te dit que si a et b commutent, alors
(a+b)^n=somme( bla bla bla)
Ici, ton problème est de calculer A^n, et tu sais que quand k>=3, B^k=0.
Voilà tout ce que tu as besoin d'avoir en tête. Il n'y a plus que deux lignes avant que tu puisses donner une expression de A^n
par Lemniscate » 17 Mar 2009, 20:07
Bonjour,
k varie de 0 à n. Ok je sors
Sinon ben je vois pas où est le problème, tu appliques la formule du binôme de Newton pour deux matrices qui commutent. Enfin, c'est de l'application quoi ! QUand on te dit d'écrire la formule, c'est juste écrire les premiers termes de la somme et trois petits points après, histoire de voir comment ça se passe... n'essaye pas de fixer une valeur pour n, n est quelconque...
Si tu n'arrives pas à résoudre cet exercice après tous ces messages, demande à ton prof de t'aider, peut être qu'en direct, tu comprendras mieux.
Bonne chance quand même.
SimonB a écrit:Oui, k varie de 1 à n et n est donné par l'énoncé (il est quelconque, mais fixé). Ca ne pose donc pas trop de problèmes...
k varie de 0 à n. Ok je sors
Sinon ben je vois pas où est le problème, tu appliques la formule du binôme de Newton pour deux matrices qui commutent. Enfin, c'est de l'application quoi ! QUand on te dit d'écrire la formule, c'est juste écrire les premiers termes de la somme et trois petits points après, histoire de voir comment ça se passe... n'essaye pas de fixer une valeur pour n, n est quelconque...
Si tu n'arrives pas à résoudre cet exercice après tous ces messages, demande à ton prof de t'aider, peut être qu'en direct, tu comprendras mieux.
Bonne chance quand même.
par juju78 » 20 Mar 2009, 18:12
On a
^n B^0 + {n \choose 1}(3I)^{n-1}B^1+{n \choose 2}(3I)^{n-2}B^2+{n \choose 3}(3I)^{n-3}B^3+........+{n \choose n}(3I)^0B^n)
On sait qu'a partir de B^3 on a B = matrice nulle
donc :
^n B^0 + {n \choose 1}(3I)^{n-1}B^1+{n \choose 2}(3I)^{n-2}B^2)
?
Car les autres termes étant multiplié par B^3, B^4 etc.. ca vaut 0 ?
On sait qu'a partir de B^3 on a B = matrice nulle
donc :
Car les autres termes étant multiplié par B^3, B^4 etc.. ca vaut 0 ?
par fatal_error » 20 Mar 2009, 18:49
oui,
sauf que ca :
c'est faux.
On sait qu'a partir de k=3, on a B^k qui est la matrice nulle.
B n'est pas la matrice nulle!
généralement on retrouve plutot la formulation
pour k >=3, B^k est la matrice nulle
sauf que ca :
On sait qu'a partir de B^3 on a B = matrice nulle
c'est faux.
On sait qu'a partir de k=3, on a B^k qui est la matrice nulle.
B n'est pas la matrice nulle!
généralement on retrouve plutot la formulation
pour k >=3, B^k est la matrice nulle
la vie est une fête
par juju78 » 20 Mar 2009, 18:57
Oui je me suis mal exprimée, on a donc B^3 = 0, B^4 = 0 , B^5 = 0 ... soit
comme vous l'avez dit pour k >=3, B^k est la matrice nulle
et donc si pour k=>3 B^k = 0 alors on a :
?
comme vous l'avez dit pour k >=3, B^k est la matrice nulle
et donc si pour k=>3 B^k = 0 alors on a :
par leon1789 » 20 Mar 2009, 19:36
Ok, mais il faut encore calculer les coefficients binomiaux de cette somme
Et que vaut (3I)^k ?
Et que vaut (3I)^k ?
80 messages
- Page 2 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :