Matrices
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
y6227
- Membre Naturel
- Messages: 26
- Enregistré le: 13 Nov 2011, 06:08
-
 par y6227 » 06 Juin 2012, 09:14
par y6227 » 06 Juin 2012, 09:14
Bonjour,
L'exercice consiste à démontrer ceci :
^3 = AB^3A^{-1})
A et B étant des matrices de taille n * n inversibles.
je ne comprends pas la correction qui est celle ci :
^3 = ABA^{-1} ABA^{-1} ABA^{-1} = AB^3A^{-1})
En effet, je dois donc comprendre que
^3 = A^{-1})
Pourquoi ceci ?
Merci d'avance
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 06 Juin 2012, 09:23
par Dinozzo13 » 06 Juin 2012, 09:23
Salut !
Que vaut
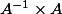
?
-
y6227
- Membre Naturel
- Messages: 26
- Enregistré le: 13 Nov 2011, 06:08
-
 par y6227 » 06 Juin 2012, 09:26
par y6227 » 06 Juin 2012, 09:26
Dinozzo13 a écrit:Salut !
Que vaut
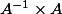
?
In cependant

ne vaut pas In non ?
-
y6227
- Membre Naturel
- Messages: 26
- Enregistré le: 13 Nov 2011, 06:08
-
 par y6227 » 06 Juin 2012, 09:28
par y6227 » 06 Juin 2012, 09:28
y6227 a écrit:In cependant

ne vaut pas In non ?
Ah oui OK c'est bon merci! je pensais qu'il fallait prouver que c'était égale à
^3A^{-1})
d'où mon incompréhension.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 06 Juin 2012, 09:32
par Dinozzo13 » 06 Juin 2012, 09:32
Dinozzo13 a écrit:Salut !
Que vaut
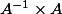
?
Si
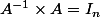
alors
^3 =(ABA^{-1}) \times (ABA^{-1})\times (ABA^{-1})=AB(A^{-1}\times A) B (A^{-1}\times A) B A^{-1}=AB I_n B I_n B A^{-1}= ...)
car le produit matriciel est associatif.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 06 Juin 2012, 09:33
par Dinozzo13 » 06 Juin 2012, 09:33
y6227 a écrit:Ah oui OK c'est bon merci! je pensais qu'il fallait prouver que c'était égale à
^3A^{-1})
d'où mon incompréhension.
ok :+++: :+++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités