Matrices
32 messages
- Page 1 sur 2 - 1, 2
Matrices
Bonjour à tous, j'aurais besoin de votre aide sur un exercice composé de matrice.
Voici la fonction f : R3[X] -> R3[X]
P(X) -> P'(X)+XP(1)
f est un endomorphisme.
Sa matrice est :
0 1 0 0
1 1 3 1
0 0 0 3
0 0 0 0
Déterminer le rang de cette matrice et une base de Imf.
Le rang je crois que c'est 3 si je ne me trompe pas mais je ne sais pas vraiment le démontrer. Et pour la base de l'image, comment dois-je procéder s'il vous plait ?
Voici la fonction f : R3[X] -> R3[X]
P(X) -> P'(X)+XP(1)
f est un endomorphisme.
Sa matrice est :
0 1 0 0
1 1 3 1
0 0 0 3
0 0 0 0
Déterminer le rang de cette matrice et une base de Imf.
Le rang je crois que c'est 3 si je ne me trompe pas mais je ne sais pas vraiment le démontrer. Et pour la base de l'image, comment dois-je procéder s'il vous plait ?
Bonjour,
il faut revenir à la définition du rang : dimension de l'espace vectoriel engendré par les lignes (ou les colonnes). On a donc

(en enlevant successivement le vecteur ligne et colonne qui est linéairement dépendant des autres ou nul).
Il est facile de voir que le rang de la dernière matrice est (tu peux calculer le déterminant).
(tu peux calculer le déterminant).
il faut revenir à la définition du rang : dimension de l'espace vectoriel engendré par les lignes (ou les colonnes). On a donc
(en enlevant successivement le vecteur ligne et colonne qui est linéairement dépendant des autres ou nul).
Il est facile de voir que le rang de la dernière matrice est
Mister Red a écrit:Si je calcule le déterminant, j'aurais quelle information sur le rang ?
Salut,
si le déterminant est non nul, ta matrice est inversible, donc son rang vaut...
Sinon, le rang d'une matrice est égal à l'ordre de la plus grande sous-matrice carrée inversible de ta matrice. A démontrer !
Le déterminant de la matrice que tu cites vaut 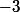 (mais peut importe, tant qu'il est non nul).
(mais peut importe, tant qu'il est non nul).
En ce qui concerne l'image, tu sais qu'elle est engendrée par les vecteurs colonne de ta matrice. Le problème est que, en général, cette famille est seulement génératrice, mais pas toujours libre.
Comme le troisième vecteur vaut 3 fois le premier, l'espace engendré reste le même si on le retire. Il reste donc trois vecteurs et comme la matrice est de rang trois.
En ce qui concerne l'image, tu sais qu'elle est engendrée par les vecteurs colonne de ta matrice. Le problème est que, en général, cette famille est seulement génératrice, mais pas toujours libre.
Comme le troisième vecteur vaut 3 fois le premier, l'espace engendré reste le même si on le retire. Il reste donc trois vecteurs et comme la matrice est de rang trois.
Je suis d'accord : c'est une base mais il y a en a "plein". C'est pour cela qu'il est impropre de parler de la base, à moins bien sûr de fixer une condition sur celle-ci.
D'ailleurs, je viens de revenir sur le premier message où il est question de polynômes : il serait préférable d'écrire une base avec des polynômes.
D'ailleurs, je viens de revenir sur le premier message où il est question de polynômes : il serait préférable d'écrire une base avec des polynômes.
32 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
