Matrices symétriques positives
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 11 Mai 2008, 13:12
par Skullkid » 11 Mai 2008, 13:12
Bonjour à tous, j'essaye de me replonger avec enthousiasme dans les espaces euclidiens, mais je bute sur l'exo que voici :
Soit
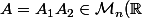)
avec

et
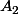
symétriques réelles positives. Montrer que
^{\frac1n})
. On pourra commencer par le cas où

est définie positive.
La première question de l'exercice consistait à montrer cette inégalité pour A symétrique positive. Donc en reprenant ce résultat on obtient
^{\frac1n} \le \frac1n trA_1\ trA_2)
. Donc j'aimerais bien montrer que
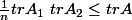
mais j'arrive à rien.
Merci d'avance.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 11 Mai 2008, 14:11
par ThSQ » 11 Mai 2008, 14:11
Déjà si y'en a une qui n'est pas > 0 c'est évident.
Ensuite écris A_1 = tP D P et A_2 = tP B P avec D diagonale et applique l'inégalité entre les moyennes.
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 11 Mai 2008, 15:51
par Skullkid » 11 Mai 2008, 15:51
Si j'appelle

les valeurs propres de

j'obtiens :
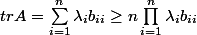^{\frac1n}=n(\det A_1)^{\frac1n}\(\prod_{i=1}^n b_{ii}\)^{\frac1n})
.
A-t-on
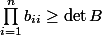
? Ou est-ce que je fais encore fausse route ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités