Matrices symetrique et antisymétrique

par **barbu23** » 22 Oct 2012, 22:28

Bonsoir à tous,

A quoi sert le fait de savoir qu'une matrice s'écrit de façon unique comme somme d'une matrice symétrique et d'une autre antisymétrique ?
Connaissez vous quelques applications de ce théorème dans le domaine de diagonalisation ?

Merci d'avance. :happy3:

par **barbu23** » 22 Oct 2012, 22:58

Bonsoir,

Pourquoi :

: l'ensemble des matrices carrés d'ordre

.

: l'ensemble des matrices carrés, antisymétriques, d'ordre

.

: l'ensemble des matrices carrés, symétriques, d'ordre

.
Je sais que

, parce que

:

Mais, je ne sais pas montrer que la somme est directe ?

Merci pour votre aide.

par **Le_chat** » 22 Oct 2012, 23:03

Si A est symétrique et antisymétrique alors tA=...

par **barbu23** » 22 Oct 2012, 23:11

Le_chat a écrit:Si A est symétrique et antisymétrique alors tA=...

Ah oui, c'est vrai donc : il faut montrer que :

.

:

est symétrique, c'est à dire :

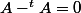
, et

est antisymétrique, c'est à dire :

.
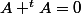
Par conséquent :

D'où le résultat.
Merci Le_chat. :happy3:

par **barbu23** » 22 Oct 2012, 23:13

Pouvez vous me donner la réponse au premier post ?
Merci d'avance. :happy3:

par **Supernova** » 22 Oct 2012, 23:14

dim A_n= n(n-1)/2 et dim S_n=n(n+1)/2 leur somme est égale à n^2 = dim M_n(IK)

par **wserdx** » 22 Oct 2012, 23:22

Il y a des applications, comme le fait que toute matrice est le produit d'une matrice symétrique et d'une matrice orthogonale.

par **barbu23** » 22 Oct 2012, 23:57

On utilise la diagonalisation dans ces applications de ce théorème ?

par **barbu23** » 23 Oct 2012, 00:09

En fait, mon vrai problème est celui qui se trouve ici : http://www.les-mathematiques.net/phorum/read.php?3,784250
Merci pour votre aide. :happy3:

par **wserdx** » 23 Oct 2012, 11:38

Par exemple décomposer en trois:
-les matrices diagonales
-les matrices triangulaires supérieures (sans diagonale)
-idem inférieures.

par **barbu23** » 23 Oct 2012, 18:26

wserdx a écrit:Par exemple décomposer en trois:
-les matrices diagonales
-les matrices triangulaires supérieures (sans diagonale)
-idem inférieures.

@wserdx :
J'ai développé quelques idées ici : http://www.maths-forum.com/dualite-trialite-132482.php
:happy3:

Matrices symetrique et antisymétrique

Matrices symetrique et antisymétrique

Qui est en ligne