Matrices: semi-diagonalisation

[pestre]

Bonjour à tous

Quelqu'un pourrait-il m'expliquer la décomposition en cellule de Jordan (ou semi-diagonalisation) des matrices carrées ?

P

[arnaud32]

Bonjour,

Ca consiste à decouper l'espace en sous espaces propres; et a deomposer sur cet espace ton application en ou est un endomorphisme nilpoten (ie tu peux trouver p tel que ).

[Finrod]

mmm arnaud,

t'es pas en train de parler de trigonalisation et d'espaces caractéristiques là plutôt ?

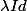+ nilpotent, c'est pas diagonalisable donc l'espace propre est strictement niclus dans l'espace caractéristique.

Puis cette histoire de semi-diagonalisabilité, c'est bof, c'est une déf moyennement pertinente, dans la mesure ou le sens ne saute pas au yeux.
(il me semble que c'est non diagonalisable mais diagonalisable dans une clôture algébrique, mais j'ai un gros doute)

[arnaud32]

En effet il s'agit des espaces caracteristques.
Mais il me semble que c'est ce que fait la reduction de Jordan.
C'est en tout cas ce que j'ai suppose, n'ayant jamais entendu parle de semi-diagonalisation.

Desole si j'ai repondu a cote de la question.

[Ben314]

Salut,
@ Finrod : si on parle effectivement de "la décomposition en blocs de Jordan", (c'est ce dont parle Arnaud) en général on écrit déjà la "théorie" dans un corps algébriquement clos.
Une matrice du style
1 1
0 1
tu peut la plonger dans absolument ce que tu veut comme corps, elle sera jamais diagonalisable.

[Finrod]

Oui justement, dans le cas présent, le terme semi-diagonalisation semblait désigner autre chose.

Et comme tu le fais remarquer, on n'a aucune chance de trigonaliser une matrice semi-diagonalisable autrement que dans un corps algébriquement clot, les valeurs propres étant sur la diagonale...