je sèche complétement pour cette question :
Matrices nilpotentes
13 messages
- Page 1 sur 1
bonjour,
si M est nilpotente, alors M annule un polynome scindé donc est trigonalisable. De plus 0 est l'unique valeur propre de M.
Dans l'autre sens, si M est trigonalisable avec des zéros sur la diagonale supérieure, alors son polynôme caractéristique va être (-1)^n*x^n d'ou il est facile ensuite d'en déduire que M est nilpotente.
si M est nilpotente, alors M annule un polynome scindé donc est trigonalisable. De plus 0 est l'unique valeur propre de M.
Dans l'autre sens, si M est trigonalisable avec des zéros sur la diagonale supérieure, alors son polynôme caractéristique va être (-1)^n*x^n d'ou il est facile ensuite d'en déduire que M est nilpotente.
Bonjour, jai enfin trouvé une preuve pour la dernière implication
. Mais je ne me suis pas servi des résultats sur les noyaux (enfin je pense
)
Pouvez vous me dire si ma preuve est juste, et si tel est le cas, est-ce que je me servirai inconsciemment des résultats précédents ?
Voici la réponse que jai trouvée :
On procède par récurrence, en posant pour tout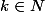 ,
, 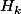 : Il existe une base B de E dans laquelle la matrice de n lignes de u soit triangulaire supérieure et les éléments diagonaux de celle-ci sont tous non nuls.
: Il existe une base B de E dans laquelle la matrice de n lignes de u soit triangulaire supérieure et les éléments diagonaux de celle-ci sont tous non nuls.
Pour n = 1.
u est nilpotent. Donc une matrice de u dans nimporte quelle base est a, avec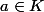 .
.
Or on sait quil existe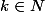 tel que
tel que 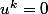 .
.
Donc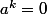 = 0
= 0
Donc a = 0
Donc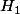 est vraie
est vraie
Soit n tel que pour tout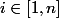 ,
, 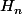 soit vraie.
soit vraie.
Dans nimporte quelle base c, 0 = det(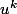 ) = det(u)
) = det(u)
Donc le déterminant de la matrice est nul dans nimporte quelle base.
Autrement dit, u est non injective
Donc il existe) non nul.
non nul.
Comme E est de dimension finie égale à n, le théorème de la base incomplète assure quil existe \in K^{n - 1} /\left\{ {x,e_2 ,...,e_n } \right\}) . On pose
. On pose 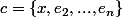 .
.
 = \left( {\begin{array} 0 & B \\ 0 & A \\\end{array}} \right)) où B est une matrice ligne de n-1 colonne et A une matrice carré de n-1 lignes.
où B est une matrice ligne de n-1 colonne et A une matrice carré de n-1 lignes.
Or on sait que^k = 0) .
.
Or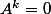
Donc A, qui est la matrice dun endomorphisme v sur le sous-espace vectoriel F = Vect(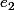 ,..,
,..,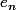 ), est nilpotente.
), est nilpotente.
Or F est un sous-espace vectoriel de dimension n-1.
En appliquant notre hypothèse de récurrence, on peut trouver une base b dans laquelle la matrice de v soit triangulaire supérieure.
Donc la matrice dans la base de E quest est une matrice triangulaire supérieure avec des zéros sur la diagonale.
est une matrice triangulaire supérieure avec des zéros sur la diagonale.
Pouvez vous me dire si ma preuve est juste, et si tel est le cas, est-ce que je me servirai inconsciemment des résultats précédents ?
Voici la réponse que jai trouvée :
On procède par récurrence, en posant pour tout
Pour n = 1.
u est nilpotent. Donc une matrice de u dans nimporte quelle base est a, avec
Or on sait quil existe
Donc
Donc a = 0
Donc
Soit n tel que pour tout
Dans nimporte quelle base c, 0 = det(
Donc le déterminant de la matrice est nul dans nimporte quelle base.
Autrement dit, u est non injective
Donc il existe
Comme E est de dimension finie égale à n, le théorème de la base incomplète assure quil existe
Or on sait que
Or
Donc A, qui est la matrice dun endomorphisme v sur le sous-espace vectoriel F = Vect(
Or F est un sous-espace vectoriel de dimension n-1.
En appliquant notre hypothèse de récurrence, on peut trouver une base b dans laquelle la matrice de v soit triangulaire supérieure.
Donc la matrice dans la base de E quest
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
