Matrice et vecteur propre

par **aston** » 04 Juin 2007, 12:48

Bonjour,

J'ai une matrice réelle

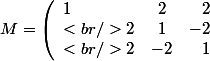et je dois vérifier, en appliquant directement la définition d'un vecteur propre (

??) que le vecteur

est vecteur propre de M.

Comment puis-je procéder sans devoir passer par les calculs fastidieux

?

Merci d'avance.

par **thomasg** » 04 Juin 2007, 12:51

bonjour,

effectue le produit de la matrice par le vecteur, tu trouveras k fois le vecteur en résultat.

A bient^to.

par **aston** » 04 Juin 2007, 12:56

thomasg a écrit:bonjour,

effectue le produit de la matrice par le vecteur, tu trouveras k fois le vecteur en résultat.

A bient^to.

J'obtiens le vecteur

(k = -3 ?!), mais en quoi celà m'aide t-il à répondre à la question ? A savoir, est ce que le vecteur

est vecteur propre de M ?

EDIT: oui bon, comme le vecteur est proportionnel c'est qu'il est vecteur propre.

Merci.

par **thedream01** » 04 Juin 2007, 13:17

Oui, bein ça te dit exactement que -3 est une valeur propre et (-1,1,1) vecteur propre associé à la valeur propre -3! c'est la définition...