Matrice d'un vecteur dans une base

[azf]

Bonjour

Soit un -espace vectoriel e dimension finie

une base de

un vecteur de

Ma question:

Est-il permis de considérer que considérer que est aussi une application linéaire?

Étant donné qu'on peut parler de la matrice de dans la base par l'expression

et étant donné qu'on parle uniquement de matrice d'une application linéaire

Mais alors si on peut par-là considérer que le vecteur est aussi une application linéaire

Comment la décrire?

C'est une application linéaire de quel ensemble de départ vers quel ensemble d'arrivée?

[azf]

et étant donné qu'on parle uniquement de matrice d'une application linéaire

ou alors on ne parle pas uniquement de matrice d'une application linéaire dans un couple de bases mais aussi et donc selon un autre contexte de matrice d'un vecteur dans une base

Comme je dois continuer je vais admettre cela

De toute façon je ne vois pas comment considérer qu'un vecteur soit aussi une application linéaire dans un couple de bases (c'est absurde)

[Maxymyze]

Vous pouvez considérer qu'une matrice uniligne ou unicolonne représente ... tout ce que vous voulez, pourvu que la représentation matricielle soit pertinente dans le contexte.
Par exemple, une matrice uniligne peut être
- un vecteur dans une base ,
- une forme linéaire définie sur R^n, etc.

[Maxymyze]

Plus précisément :
En soi, une matrice n'est jamais qu'une application définie sur le produit cartésien de deux ensembles finis.
Par ex., une matrice uniligne à n éléments est une application
{1} X {1, 2, ..., n}
C'est le contexte qui donne un autre sens à la matrice.

[Maxymyze]

"Est-il permis de considérer que considérer que est aussi une application linéaire?"
Non. Mais la matrice de x pourquoi pas.

[azf]

Merci Maxymyse

Donc si je comprends bien il faut prendre la définition

On appelle "matrice d'un vecteur dans une base", la matrice colonne des coordonnées d'un vecteur dans une base

sans chercher à y voir autre chose plus que ce qu'elle dit

[azf]

"Est-il permis de considérer que considérer que est aussi une application linéaire?"
Non. Mais la matrice de x pourquoi pas.

ah bah oui effectivement (je suis complètement stupide de ne pas y avoir pensé)!!!

Encore merci pour cette précision Maxymyse

[Maxymyze]

"e" est il une voyelle, la constante d'Euler ou le symbole de l'électron ?
Cela dépend de ce qu'on en fait.
Idem pour les matrices.

[azf]

Bonne soirée à vous Maxymyse

Vous m'avez vraiment aidé à voir plus clair

je n'avais pas pensé (et c'est stupide de ma part) que la matrice du vecteur dans la base définie par



peut être aussi vu comme la matrice d'une application linéaire dans un couple de bases sans pour autant considérer que le vecteur x soit une application linéaire pour autant

[Ben314]

Salut,

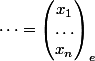
Normalement et en réfléchissant un peu, je pense que tu pourrait trouver tout seul la réponse à ta question :
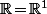
Ta matrice, elle est de taille donc elle représente une application linéaire de dans et, plus précisément, elle représente l'application .
Et quel est le lien avec le vecteur de départ ? ben cette application c'est l'application .

Tu verra plus tard qu'étant donné un espace vectoriel E sur un corps K, on considère très souvent l'ensemble des applications linéaires de E dans K (qu'on appelle le dual de E), mais qu'on ne parle que trés rarement de l'ensemble des applications linéaires de K dans E (qui n'a pas de nom).
Et la raison toute bête, c'est que cet ensemble, ben au fond, c'est E lui même . . .

[azf]

Merci oui Ben 314

Bon à force de "bosser" mes maths ça va finir par rentrer

Je me suis posé cette question (donc question idiote pour le coup) en cherchant à généraliser des exercices "bateaux" d'algèbre linéaire donnés dans

Donc c'est ok j'ai obtenu la généralisation souhaitée que je formule ici

Soient et deux -espace vectoriels de dimensions finies

et deux bases de

et deux bases de

une application linéaire

Alors

Avec les matrices de passage et

Encore merci