Matrice
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Samba
- Membre Naturel
- Messages: 33
- Enregistré le: 31 Déc 2019, 17:31
-
 par Samba » 31 Déc 2019, 18:24
par Samba » 31 Déc 2019, 18:24
On considère la matrice
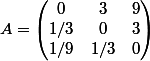
1. Calculer A²- A - 2I₃. En déduire que A est inversible et calculer
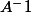
.
2. Soient B=1/3(A + I₃) et C=-1/3 (A - 2I₃). Calculer
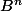
et
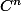
, n ∈ ℕ*
3. Calculer
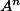
, n ∈ ℕ*
Je bloque à la question 2.
-
Samba
- Membre Naturel
- Messages: 33
- Enregistré le: 31 Déc 2019, 17:31
-
 par Samba » 31 Déc 2019, 18:33
par Samba » 31 Déc 2019, 18:33
Je veux appliquer la formule du binôme de Newton mais je fais comment si la matrice A ne s'annule pas par son propre produit ?
-
Samba
- Membre Naturel
- Messages: 33
- Enregistré le: 31 Déc 2019, 17:31
-
 par Samba » 31 Déc 2019, 20:27
par Samba » 31 Déc 2019, 20:27
De l'aide ?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 31 Déc 2019, 20:40
par GaBuZoMeu » 31 Déc 2019, 20:40
si la matrice A ne s'annule pas par son propre produit ?
Qu'est-ce que ça veut dire ?
As-tu calculé
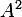
, pour commencer ? (en utilisant
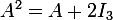
)
-
Samba
- Membre Naturel
- Messages: 33
- Enregistré le: 31 Déc 2019, 17:31
-
 par Samba » 31 Déc 2019, 21:37
par Samba » 31 Déc 2019, 21:37
-
mathelot
 par mathelot » 31 Déc 2019, 22:21
par mathelot » 31 Déc 2019, 22:21
Factoriser le trinôme
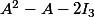
En déduire que
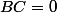
Que vaut
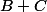
?
Comment se simplifie le développement du binôme
^n)
?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 01 Jan 2020, 10:26
par GaBuZoMeu » 01 Jan 2020, 10:26
Bonne année,
Je corrige la coquille dans mon indication : je voulais écrire : as-tu calculé
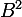
pour commencer, en utilisant
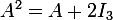
?
-
mathelot
 par mathelot » 01 Jan 2020, 11:36
par mathelot » 01 Jan 2020, 11:36
On peut factoriser
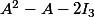
en s'aidant de l'identité
(x+1))
-
Samba
- Membre Naturel
- Messages: 33
- Enregistré le: 31 Déc 2019, 17:31
-
 par Samba » 01 Jan 2020, 14:07
par Samba » 01 Jan 2020, 14:07
-
Samba
- Membre Naturel
- Messages: 33
- Enregistré le: 31 Déc 2019, 17:31
-
 par Samba » 01 Jan 2020, 14:10
par Samba » 01 Jan 2020, 14:10
Où tu veux en venir mathelot ?
-
mathelot
 par mathelot » 01 Jan 2020, 14:16
par mathelot » 01 Jan 2020, 14:16
Calculons et developpons
 ^n)
Comme BC=0 de nombreux termes du développement du binôme vont se simplifier.
Notons que B et C commutent.
On va en déduire une égalité avec B^n et C^n
Modifié en dernier par mathelot le 01 Jan 2020, 14:31, modifié 2 fois.
-
Samba
- Membre Naturel
- Messages: 33
- Enregistré le: 31 Déc 2019, 17:31
-
 par Samba » 01 Jan 2020, 14:20
par Samba » 01 Jan 2020, 14:20
-
Samba
- Membre Naturel
- Messages: 33
- Enregistré le: 31 Déc 2019, 17:31
-
 par Samba » 01 Jan 2020, 14:28
par Samba » 01 Jan 2020, 14:28
mathelot a écrit:Calculons et developpons
(B+C) ^n
Comme BC=0 de nombreux termes du développement du binôme vont se simplifier.
Notons que B et C commutent.
Je sais pas faire les symboles de la somme et de la combinaison en latex. Tu m'envoies les codes ?
-
mathelot
 par mathelot » 01 Jan 2020, 14:37
par mathelot » 01 Jan 2020, 14:37
-
mathelot
 par mathelot » 01 Jan 2020, 14:41
par mathelot » 01 Jan 2020, 14:41
Samba a écrit: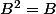
Qu'est ce que l'on en déduit par récurrence ?
-
Samba
- Membre Naturel
- Messages: 33
- Enregistré le: 31 Déc 2019, 17:31
-
 par Samba » 01 Jan 2020, 15:05
par Samba » 01 Jan 2020, 15:05
mathelot a écrit: Samba a écrit: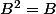
Qu'est ce que l'on en déduit par récurrence ?
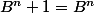
? (désolé pour le "+1" qui n'apparait pas comme un exposant)
-
Samba
- Membre Naturel
- Messages: 33
- Enregistré le: 31 Déc 2019, 17:31
-
 par Samba » 01 Jan 2020, 15:10
par Samba » 01 Jan 2020, 15:10
Dois je pas savoir pour quelle valeur valeur de n m’arrêter dans mon développement du binôme ?
-
mathelot
 par mathelot » 01 Jan 2020, 15:13
par mathelot » 01 Jan 2020, 15:13
-
GaBuZoMeu
- Habitué(e)
- Messages: 6134
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 01 Jan 2020, 15:23
par GaBuZoMeu » 01 Jan 2020, 15:23
OK Samba. Et que se passe-t-il pour
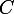
?
-
mathelot
 par mathelot » 01 Jan 2020, 15:26
par mathelot » 01 Jan 2020, 15:26
Samba a écrit:Dois je pas savoir pour quelle valeur valeur de n m’arrêter dans mon développement du binôme ?
Dès qu'il y a le produit BC dans un terme du binôme, le terme est nul.
Que reste il du développement du binôme après la simplification BC=0 ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
en s'aidant de l'identité
pour commencer, en utilisant
?