Bonjour,
J ai un probleme avec cet exercice:
M_2= -1 -1
-1 -1
matrice d ordre 2 et
A= M - 2I, I matrice unité d'ordre 2.
a)calculer M^2, M^3 puis M^k, k entier
b)montrer par récurrence que A^n =Un I+Vn M. Pour tout n entier.
Donner les expressions des suites Un et Vn en fonction de n.
alors voila je coince a partir de la question b):
j arrive a trouver que Un est une suite geométrique :Un= (-2)^n,j ai du mal à sortir l expression de (Vn),merci d'avance
Matrice
11 messages
- Page 1 sur 1
Re: matrice
par zygomatique » 09 Aoû 2016, 17:16
salut
ben quelles relations de récurrence obtiens-tu entre les u_n et v_n ?
ben quelles relations de récurrence obtiens-tu entre les u_n et v_n ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: matrice
par ariel60 » 09 Aoû 2016, 18:21
je trouve que Un+1=-2 Un et Vn+1=Un-4Vn
j arrive pas à sortir l'expression de (Vn)
Coridalement.
j arrive pas à sortir l'expression de (Vn)
Coridalement.
Re: matrice
par zygomatique » 09 Aoû 2016, 18:57
bon il y a un truc ... mais je ne m'en souviens plus ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: matrice
par aymanemaysae » 09 Aoû 2016, 20:01
Bonjour,
pour que mes calculs n' interférent pas avec les calculs de M.Zygomatique et Mlle Ariel60, je vais aborder un calcul direct de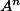
et non un calcul par récurrence .
On trouve que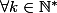
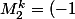: ^k 2^{k-1}\begin{pmatrix} 1&1\\1&1 \end {pmatrix} = (-2)^{k-1} M)
, sans oublier que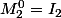 
,
et comme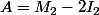
, donc pour tout 
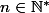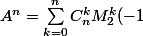: ^{n-k} 2^{n-k})
=^n 2^n I_2 + (-2)^{n-1} M \sum_{k=1}^n C_n^k)
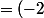^n I_2 + (-2)^{n-1}(2^n-1) M)
, sans oublier que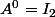 
.
Ceci donne que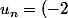^n)
et 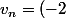^{n-1}(2^n-1))
pour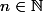 
.
J'espère que cela éclairera la chemin de récurrence .
Bon courage .
pour que mes calculs n' interférent pas avec les calculs de M.Zygomatique et Mlle Ariel60, je vais aborder un calcul direct de
On trouve que
et comme
=
Ceci donne que
J'espère que cela éclairera la chemin de récurrence .
Bon courage .
Modifié en dernier par aymanemaysae le 10 Aoû 2016, 10:48, modifié 2 fois.
Re: matrice
par ariel60 » 10 Aoû 2016, 05:59
Je ne vois pas comment sortir Vn de Vn+1=Un-4Vn. ..
j'ai trouvé que Vo=0
j'ai trouvé que Vo=0
Re: matrice
par Pseuda » 10 Aoû 2016, 06:37
ariel60 a écrit:Je ne vois pas comment sortir Vn de Vn+1=Un-4Vn. ..
j'ai trouvé que Vo=0
Bonjour,
Tu peux exprimer
Puis il ne reste plus qu'à calculer la puissance de cette matrice : il faut d'abord la diagonaliser, soit l'exprimer sous la forme
Re: matrice
par Robot » 10 Aoû 2016, 20:57
Une autre possibilité :
Mettons que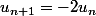
et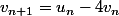 
soient corrects (je n'ai pas vérifié).
Alors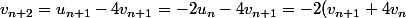-4v_{n+1}=-6v_{n+1}-8v_n.)
(On obtient une récurrence linéaire d'ordre 2 sur les
en éliminant les 
).
On cherche une base de l'espace des suites vérifiant cette récurrence linéaire d'ordre 2 formée de suites géométriques en résolvant l'équation caractéristique aux raisons :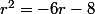
, et puis ça roule ...
Mettons que
Alors
(On obtient une récurrence linéaire d'ordre 2 sur les
On cherche une base de l'espace des suites vérifiant cette récurrence linéaire d'ordre 2 formée de suites géométriques en résolvant l'équation caractéristique aux raisons :
Re: matrice
par aymanemaysae » 10 Aoû 2016, 22:47
Bonsoir;
Bravo M.Robot , j'étais si ravi que j'ai applaudi : c'est une méthode à apprendre par cœur .
Je suis aussi content parce que votre méthode aboutit aux résultats que j'ai obtenus plus haut .
Bien sur , il y ' a d'autres méthodes , mais elles ne sont pas aussi subtiles que celle-ci .
Merci.
Bravo M.Robot , j'étais si ravi que j'ai applaudi : c'est une méthode à apprendre par cœur .
Je suis aussi content parce que votre méthode aboutit aux résultats que j'ai obtenus plus haut .
Bien sur , il y ' a d'autres méthodes , mais elles ne sont pas aussi subtiles que celle-ci .
Merci.
Re: matrice
par Robot » 11 Aoû 2016, 08:42
Aymane, réserve ton enthousiasme aux choses qui en valent la peine et ne gâche pas ta mémoire à apprendre par coeur cette astuce ! Il vaut mieux comprendre que cette astuce n'est qu'un truc pour utiliser sans le dire le polynôme caractéristique de la matrice donnant la récurrence.
Re: matrice
par aymanemaysae » 11 Aoû 2016, 09:45
Bonjour,
c'est une façon de vous témoigner ma gratitude : vous contribuez à aider beaucoup de gens gratuitement , alors que je connais d'autres qui quand ils ouvrent la bouche ils font tourner leur compteur.
Encore une fois Merci.
Voici une autre méthode pour résoudre cet exercice:
On a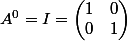
, 
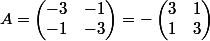et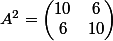 
.
Conjecturons que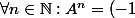^n \begin {pmatrix}a_n&b_n\\b_n&a_n \end {pmatrix})
avec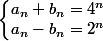 
et calculons 
.
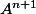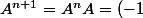^n \begin {pmatrix}a_n&b_n\\b_n&a_n \end {pmatrix} \begin {pmatrix}-3&-1\\-1&-3 \end {pmatrix} = (-1)^{n+1} \begin {pmatrix} 3a_n+b_n&a_n+3b_n\\a_n+3b_n&3a_n+b_n \end {pmatrix})
.
Posons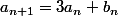
et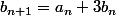 
,
donc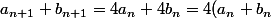 = 4^{n+1})
,
et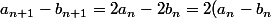 = 2^{n+1})
,
donc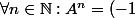^n \begin {pmatrix}a_n&b_n\\b_n&a_n \end {pmatrix})
avec .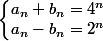
On a :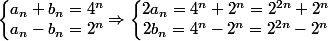
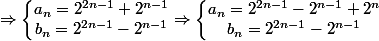
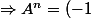^n \begin {pmatrix} 2^{2n-1}-2^{n-1}+2^n&2^{2n-1}-2^{n-1}\\2^{2n-1}-2^{n-1}&2^{2n-1}-2^{n-1}+2^n \end {pmatrix})
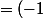^n \big( 2^n \begin {pmatrix}1&0\\0&1\end {pmatrix} + (2^{2n-1}-2^{n-1})\begin {pmatrix}1&1\\1&1\end {pmatrix}) = (-1)^n (2^n I - 2^{n-1}(2^n-1)M))
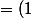^n 2^n I + (-1)^{n-1} 2^{n-1}(2^n-1)M = (-2)^n I +(-2)^{n-1}(2^n-1)M)
.
c'est une façon de vous témoigner ma gratitude : vous contribuez à aider beaucoup de gens gratuitement , alors que je connais d'autres qui quand ils ouvrent la bouche ils font tourner leur compteur.
Encore une fois Merci.
Voici une autre méthode pour résoudre cet exercice:
On a
Conjecturons que
Posons
donc
et
donc
On a :
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :