Matrice
97 messages
- Page 3 sur 5 - 1, 2, 3, 4, 5
pluie2 a écrit:d'accord le calcul me parait assez difficile....
(2I2+N)^n = somme de k=0 à n de (2I2)^n*N^(n-k)
= (2I2)^n*somme de k=0 à de N^(n-k)
=(2I2)^n*somme de k=0 à de
j'aimerais exprimer la somme avec une suite géométrique est ce possiblee ici?
Essaie d'utiliser le langage
Trouve le plus petit entier
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
pluie2 a écrit:je ne sais pas comment l'utiliser
je trouve un p=2
Tu peux voir ça ici :++:
Très bien, donc pour
Sachant que d'après la formule du binôme de Newton, on a
tu as alors
Je te laisse trouver donc
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
pluie2 a écrit:mais dans votre formule et développement, qui est A^n et A (1 parmi n)?
Je ne comprends pas, ce tu veux dire.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
A cause de ça :
capitaine nuggets a écrit:est une matrice diagonale par blocs donc, en posant
et
, on a :
.
Lessignifie que tous les termes, en dehors des matrices
et
sont nuls.
Exprime alorsen fonction de
, sachant que
où
est une matrice nilpotente i.e. à partir d'une certaine puissance
, N
. Il sera donc facile d'obtenir
en calculant
grâce à la formule du binôme de Newton :+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
pluie2 a écrit:donc A1^n=(0 parmi n)N^0(2I2)^n+(1 parmi n)N(2I2)^(n-1)
je ne vois vraiment pas quoi écrire de mieux
Que valent
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
pluie2 a écrit:0 parmi n vaut 1
N^0 vaut I2
(2I2)^n vaut 2^n*I2^n
Oui, et que vaut
Fais-en de même avec
Déduis-en donc
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
pluie2 a écrit:I2^n vaut I2
et l'autre ligne : n*2^(n-1)*I2
donc (2I2+N)^n = I2+n*N*2^(n-1)*I2=I2+n*N*2^(n-1)
T'as dû oublier des choses :
Ainsi,
Réécris alors
Tu auras ainsi
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Presque, nous ce qu'on cherche, c'est M^n.
Il reste donc à calculer .
.
Ensuite, tu auras une expression plus détaillée de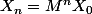 .
.
Il reste donc à calculer
Ensuite, tu auras une expression plus détaillée de
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
C'est ce que je te demande :
si tu multiplie une racine par un scalaire, multiplie tout les éléments de cette matrice par ce scalaire.
capitaine nuggets a écrit:Ainsi,.
Réécris alorssous la forme d'une matrice 2x2.
Tu auras ainsi.
si tu multiplie une racine par un scalaire, multiplie tout les éléments de cette matrice par ce scalaire.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
pluie2 a écrit:oui justement je sais bien mais je n'y arrive pas...
je ne vois pas comment passer de la forme écrite au dessus à la matrice 2*2
"i tu multiplie une racine par un scalaire, multiplie tout les éléments de cette matrice par ce scalaire." je ne vois pas comment l'appliquer ici
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
97 messages
- Page 3 sur 5 - 1, 2, 3, 4, 5
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
