Matrice puissance 2014

[Anaisdeistres]

Bonjour,

Voici ma matrice :



Et je cherche la valeur de

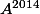
Que doit-on faire ?

Merci.

[danyL]

bonsoir
en calculant jusqu'à A^4 on a une bonne surprise

[Anaisdeistres]

Oui je sais mais quel est la formule générale ?

[FLBP]

Salut, tu devrais chercher l'espace propre pour pouvoir la diagonaliser !

[Anaisdeistres]

Salut,

Non je ne pense pas qu'il faut la diagonaliser

[aviateur]

quand on dit diagonaliser c'est pas forcément aller jusqu'au bout ici (mais en général il faut bien diagonaliser). L'idée étant de voir que les valeurs propres sont -1, -i, i. ça suffit pour voir que A^4=I et tout est là.
Ou encore, alors le polynôme caractéristique est p(x)=x^3+x^2+x+1
Comme P(A)=0 et que p(x)(x-1)=x ^4-1 alors on voit d'une autre façon que A^4=I.
Il vient alors si n=r mod 4, A^n=A^r.

[Anaisdeistres]

D'accord merci !