Matrice de passage, bloqué sur le système

[Carpate]

Les vecteurs colonnes de A étant liés, son déterminant est nul ce qui signifie qu'on ne peut pas résoudre ce système.
Le système admet une infinité de solutions : vecteurs colinéaires au vecteur
Remarque qu'on ne te demandait pas de résoudre le système ....

[Carpate]

Par ailleurs en effet je confond les deux notions si tu peux me dire si c'est bien ça :

Donc si on me donne une matrice et qu'on me demande de trouver la matrice de passage vers une autre matrice (une autre base) , il faut que je fasse comme j'ai expliqué précédemment...
avec l'histoire des systèmes a résoudre en fonction de chaque vecteurs d'arrivé.

Mais si on me donne une fonction et qu'on me demande de trouver la matrice de passage vers une autre matrice alors je ne fais pas du tout comme ça et je passe juste chaque vecteur d'arrivés en paramètres pour former au finish la matrice de passage...

Vu que la question est la même mais que c'est juste l’élément du début qui change j'ai un peu de mal a comprendre pourquoi la méthode est si différente.

Moi j'aurai eu envie de prendre le système formé par la fonction , de le résoudre en fonction de chaque vecteur de la base d'arrivé et d'en sortir une matrice de passage.

)

C'est du grand n'importe-quoi !
Tu as vraiment besoin d'un bon rappel sur les notions de base d'une application linéaire !
Ensuite mais ensuite seulement le document fourni par aymanemaysae concernant les changements de base te sera profitable.

[aymanemaysae]

Bonsoir,

je ne voulais pas le dire, mais vu que la matrice en question a un déterminant nul, le problème posé est une fiction et n'est l’œuvre d'aucun professeur et ne se trouve sur aucun manuel de Mathématiques, et qu'il est peut-être - seulement - une prouesse de l'imagination de M.Roby .

Les problèmes qui discutent des matrices de passage et des changements de coordonnées ne mettent pas en jeu des matrices dont le déterminant est nul. Si j'ai tort, je demande à M. le modérateur de supprimer mes deux interventions sur ce fil pour les bêtises qu'elles comportent.

Edit: Je m'excuse, je n'avais pas vu l'intervention de M. Carpate, qui va dans le sens de ce que j'ai avancé.
Merci.

[zygomatique]

salut

prenons l'exemple :

Ecrire la matrice de f (x; y) = (x + 2y; 4x + 8y) dans la base (1; 1); (1; 2)

f(1, 1) = (3, 12) = -6(1, 1) + 9(1, 2)

f(1, 2) =(5, 20) = -10(1, 1) + 15(1, 2)

donc la matrice de f dans la base B = {(1, 1), (1, 2)} est



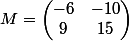
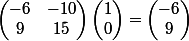
car dans la base B :: (1, 1) = 1(1, 1) + 0(1, 2) est représenté par le couple (de coordonnées) (1, 0)

(c'est pourquoi on parle de base canonique (1, 0), (0, 1) puisque ce sont les coordonnées des premier et deuxième vecteurs u et v de toute base (u, v))


donc dans la base B : (résultat dans la base canonique dans laquelle sont écrits (1, 1) et (1, 2))