Matrice non inversible
32 messages
- Page 1 sur 2 - 1, 2
matrice non inversible
bonsoir,
je suis coincé sur une question si vous pouvez m'aider la dessus:
Montrez que la dimension maximale d'un sous espace de Mn(IK) ne contenant aucune matrice inversible est n(n-1).
merci d'avance :we: .
je suis coincé sur une question si vous pouvez m'aider la dessus:
Montrez que la dimension maximale d'un sous espace de Mn(IK) ne contenant aucune matrice inversible est n(n-1).
merci d'avance :we: .
Bonsoir,
La question est... intéressante...
Je pense qu'on s'en sort en cosidérant que, si deux matrices A et B sont telles que A+tB soit non inversible pour tout t réel t, cela signifie que le déterminant de A+tB, qui est un polynôme en t, et nul pour tout t donc que tout ces coeffs sont nuls.
Sauf que le coeff en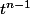 c'est...
c'est...
La question est... intéressante...
Je pense qu'on s'en sort en cosidérant que, si deux matrices A et B sont telles que A+tB soit non inversible pour tout t réel t, cela signifie que le déterminant de A+tB, qui est un polynôme en t, et nul pour tout t donc que tout ces coeffs sont nuls.
Sauf que le coeff en
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Bonsoir,
La question est... intéressante...
Je pense qu'on s'en sort en cosidérant que, si deux matrices A et B sont telles que A+tB soit non inversible pour tout t réel t, cela signifie que le déterminant de A+tB, qui est un polynôme en t, et nul pour tout t donc que tout ces coeffs sont nuls.
Sauf que le coeff enc'est...
ok merci je vais voir si je peux y arriver
Bon, ça fait une heure que je cherche à montrer... un truc faux (et qui pourtant aurait été utile pour ton truc...) à savoir :
Si et
et  sont deux matrices telles que
sont deux matrices telles que \cap\ker(B)=\{0\}) alors il existe une matrice inversible dans
alors il existe une matrice inversible dans 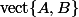
Contre exemple assez simple) et
et ) sauf que, comme j'était persuadé que c'était vrai, ben j'ai pas cherché de contre exemple...
sauf que, comme j'était persuadé que c'était vrai, ben j'ai pas cherché de contre exemple...
Mais, en voyant le contre exemple, je tenterais bien un truc du style :
Si et
et  sont deux matrices telles que
sont deux matrices telles que \cap\ker(B)=\{0\}) et
et +\text{Im}(B)={\bb R}^n) alors il existe une matrice inversible dans
alors il existe une matrice inversible dans 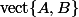
Si c'est vrai, sauf erreur, ça permettrais de conclure.
Si
Contre exemple assez simple
Mais, en voyant le contre exemple, je tenterais bien un truc du style :
Si
Si c'est vrai, sauf erreur, ça permettrais de conclure.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Bon, ça fait une heure que je cherche à montrer... un truc faux (et qui pourtant aurait été utile pour ton truc...) à savoir :
Siet
sont deux matrices telles que
alors il existe une matrice inversible dans
Contre exemple assez simpleet
sauf que, comme j'était persuadé que c'était vrai, ben j'ai pas cherché de contre exemple...
Mais, en voyant le contre exemple, je tenterais bien un truc du style :
Siet
sont deux matrices telles que
et
alors il existe une matrice inversible dans
Si c'est vrai, sauf erreur, ça permettrais de conclure.
ça reste quand meme flou.
je pense qu il faut procédé par une application injective de cet espace vers un autre de dimension egale à n(n-1) par exemple l espace {M de Mn(K) / Cn(M)=0} Cn la dernière colonne de M egale à 0 partout quelque chose comme ça
Bonjour,
Je pense que j'ai une solution (pour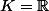 ou
ou  ...)
...)
Considérons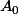 une matrice de rang maximal de notre sev
une matrice de rang maximal de notre sev  (composé uniquement de matrices non inversibles) de
(composé uniquement de matrices non inversibles) de ) . Sans perte de généralités
. Sans perte de généralités ) .
.
1) Nécessairement aucune matrice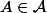 a des coefficients
a des coefficients 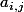 non nuls si
non nuls si  et
et  sont
sont 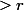 (sinon
(sinon >r) si
si  est assez petit).
est assez petit).
2) Maintenant supposons qu'il existe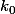 tel que
tel que 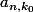 et
et 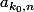 soient simultanément non nuls. Alors pour
soient simultanément non nuls. Alors pour  assez petit
assez petit >r) ce qui est impossible puisque
ce qui est impossible puisque 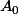 est supposé de rang maximal.
est supposé de rang maximal.
Là c'est fini puisque l'on obtient nécessairement coefficients nuls.
coefficients nuls.
Edit : Correction de nombreuses fautes de frappes.
Edit 2 : Le 2) je suis pas sûr que ça soit vrai en fait...
Je pense que j'ai une solution (pour
Considérons
1) Nécessairement aucune matrice
2) Maintenant supposons qu'il existe
Là c'est fini puisque l'on obtient nécessairement
Edit : Correction de nombreuses fautes de frappes.
Edit 2 : Le 2) je suis pas sûr que ça soit vrai en fait...
Je pense que c'est bon, mais il y a un truc à rajouter à la fin :
quand tu dit qu'il y a forcément n coeff nuls dans A, ça me semble parfaitement O.K. (en précisant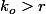 ), mais le problème, c'est qu'il faudrait montrer que les positions des fameux n coeffs nuls, c'est les même pour toutes les matrices A de l'e.v. de départ (pour le moment tu montre juste que chaque matrice a n coeff nuls).
), mais le problème, c'est qu'il faudrait montrer que les positions des fameux n coeffs nuls, c'est les même pour toutes les matrices A de l'e.v. de départ (pour le moment tu montre juste que chaque matrice a n coeff nuls).
Mais il doit suffire de considérer deux matirices A et A' où les 0 ne seraient "pas aux même endroits" puis des combinaisons linéaires des deux pour montrer que ça déconne...
quand tu dit qu'il y a forcément n coeff nuls dans A, ça me semble parfaitement O.K. (en précisant
Mais il doit suffire de considérer deux matirices A et A' où les 0 ne seraient "pas aux même endroits" puis des combinaisons linéaires des deux pour montrer que ça déconne...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Je pense que c'est bon, mais il y a un truc à rajouter à la fin :
quand tu dit qu'il y a forcément n coeff nuls dans A, ça me semble parfaitement O.K. (en précisant), mais le problème, c'est qu'il faudrait montrer que les positions des fameux n coeffs nuls, c'est les même pour toutes les matrices A de l'e.v. de départ (pour le moment tu montre juste que chaque matrice a n coeff nuls).
Mais il doit suffire de considérer deux matirices A et A' où les 0 ne seraient "pas aux même endroits" puis des combinaisons linéaires des deux pour montrer que ça déconne...
En fait
Je propose la piste suivante (mais je ne l'ai pas vérifiée complètement)
Si A et B sont deux sev de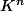 , de base respective
, de base respective 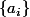 et
et 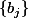 alors le sev (que je note peut-être abusivement)
alors le sev (que je note peut-être abusivement) 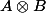 de
de )
de base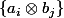 contient toutes les matrices dont l'image est contenue dans A et dont le noyau contient l'orthogonal de B.
contient toutes les matrices dont l'image est contenue dans A et dont le noyau contient l'orthogonal de B.
Réciproquement, si E est un sev de) , on définit A comme la somme des images des matrices de E, et B comme la somme des orthogonaux des noyaux des matrices de E, alors E est contenu dans
, on définit A comme la somme des images des matrices de E, et B comme la somme des orthogonaux des noyaux des matrices de E, alors E est contenu dans 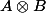
Un sev maximal ne contenant pas de matrice inversible sera donc tel que dim(A)=n dim(B)=n-1 ou bien
dim(A)=n-1 dim(B)=n
Si A et B sont deux sev de
de base
Réciproquement, si E est un sev de
Un sev maximal ne contenant pas de matrice inversible sera donc tel que dim(A)=n dim(B)=n-1 ou bien
dim(A)=n-1 dim(B)=n
Sauf erreur, pour montrer que si dim(A)=dim(B)=n alors le s.e.v. E contient forcément une matrice inversible, tu as besoin de ça :
Sauf que ça, j'y arrive pas...
non ?ben314 a écrit:Siet
sont deux matrices telles que
et
alors il existe une matrice inversible dans
Sauf que ça, j'y arrive pas...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ca, ça veut dire que tu fait l'hypothèse que le s.e.v. E se présente forcément sous la formewserdx a écrit:ben, si dim(A)=dim(B)=n, alors, d'où
, qui contient bien quelques matrices inversibles, non? ou alors je n'ai pas compris ta remarque.
d'ailleurs, tu le fait remarquer toi même :
donc ce n'est parce quewserdx a écrit:Réciproquement, si E est un sev de, on définit A comme la somme des images des matrices de E, et B comme la somme des orthogonaux des noyaux des matrices de E, alors E est contenu dans
bon, sinon, ça aussi c'est faux :
Et c'est l'exemple de mr_pyer :ben314 a écrit:Siet
sont deux matrices telles que
et
alors il existe une matrice inversible dans
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ce n'est pas une hypothèse, cela se déduit du fait que E est de dimension maximale, et que 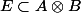 pour A et B définis dans mon post précédent.
pour A et B définis dans mon post précédent.
Il y a un point que je précise, qui n'est peut-être pas évident : toutes les matrices de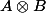
sont de rang au plus égal à min(dim(A), dim(B)). Donc en particulier si dim(A)=n, dim(B)=n-1 ou dim(A)=n-1, dim(B)=n, toutes les matrices de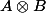
sont de rang au plus n-1, donc non inversibles.
Il y a un point que je précise, qui n'est peut-être pas évident : toutes les matrices de
sont de rang au plus égal à min(dim(A), dim(B)). Donc en particulier si dim(A)=n, dim(B)=n-1 ou dim(A)=n-1, dim(B)=n, toutes les matrices de
sont de rang au plus n-1, donc non inversibles.
Dans le cas où 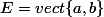 avec a et b les matrices çi dessus, on a
avec a et b les matrices çi dessus, on a 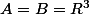 et E ne contient que des non inversibles alors que, bien sûr
et E ne contient que des non inversibles alors que, bien sûr ) contient des inversibles.
contient des inversibles.
Donc je ne vois absolument pas en quoi la "maximalisé" de E te garanti qu'il est de la forme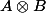 (ne pas oublier que ce que tu a le droit de supposer, c'est que E est de dimension maximale parmi les s.e.v. ne contenant que des non inversibles)
(ne pas oublier que ce que tu a le droit de supposer, c'est que E est de dimension maximale parmi les s.e.v. ne contenant que des non inversibles)
Donc je ne vois absolument pas en quoi la "maximalisé" de E te garanti qu'il est de la forme
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ce que tu est en train de dire, c'est que, partant d'un s.e.v. E quelconque de Mn(R), si on calcule ton A et ton B, alors,wserdx a écrit:Donc en particulier si dim(A)=n, dim(B)=n-1 ou dim(A)=n-1, dim(B)=n, toutes les matrices desont de rang au plus n-1, donc non inversibles.
Ca c'est O.K., mais après, c'est la réciproque que tu utilise et... elle est fausse... (contrairement à ce que j'intuitait au début...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
J'ai repris ma première idée, à savoir quelle est la dimension maximale d'un EV ne contenant que des matrices de rang au plus r ?
Pour r=1, je suis à peu près convaincu qu'un tel EV est de la forme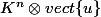 ou
ou 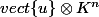 , et que donc la dimension est n.
, et que donc la dimension est n.
Pour r=2, je pense qu'un EV maximal est la somme directe de 2 EV maximaux pour r=1, la dimension serait donc 2n. Quelqu'un voit-il comment le démontrer ou bien un contre-exemple ?
Si c'est vrai, je pense également qu'on doit pouvoir démontrer par récurrence qu'un EV maximal pour r est la somme directe de r EV maximaux pour 1.
Pour r=1, je suis à peu près convaincu qu'un tel EV est de la forme
Pour r=2, je pense qu'un EV maximal est la somme directe de 2 EV maximaux pour r=1, la dimension serait donc 2n. Quelqu'un voit-il comment le démontrer ou bien un contre-exemple ?
Si c'est vrai, je pense également qu'on doit pouvoir démontrer par récurrence qu'un EV maximal pour r est la somme directe de r EV maximaux pour 1.
32 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
