Matrice magique symétrique

par **sarah79** » 13 Avr 2010, 10:04

j'ai un problème pour trouver ce qui m'est demandé : montrer qu'il existe une seule matrice magique symétrique So, So=(b ij) avec 1<=i<=3 et 1<=j<=3 telle que s(So) et b11=0.

(s(So) pour les matrices magiques c'est la valeur commune des huit somme)

J'en déduit de l'énoncé la matrice suivante :
(1 b12 b13)
(b12 b21 b22)
(b13 b22 b33)

et le systeme suivant :
1+b12+b13=0
b12+b21+b22=0
b13+b22+b33=0
1+b21+b33=0
2b13+b21=0

après je suis bloqué, je ne trouve pas qu'une seule matrice.
Pouvez vous m'aider svp?

par **girdav** » 13 Avr 2010, 10:08

Si

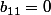
pourquoi le terme de la première ligne et première colonne vaut

?

par **sarah79** » 13 Avr 2010, 10:11

jme suis trompé en écrivant l'énoncé b11=1

par **girdav** » 13 Avr 2010, 10:19

vaut bien

d'après ce que tu écris ensuite.
Essaie d'exprimer les autres coefficients en fonction de

.
On devrait trouver

.

par **sarah79** » 13 Avr 2010, 10:24

En faisant le raisonnement avec des matrices ou en restant sous forme de systeme d'équation?

par **sarah79** » 13 Avr 2010, 10:31

Je ne comprends pas pk on ne doit trouver qu'une matrice, les différents termes s'ils sont exprimé en fonction de b12 il y aura une infinité de solution. J'ai beau refaire mon système je ne vois pas comment on trouve b12=-1 b13=0 et ainsi de suite. Comment faire le raisonnement?

par **girdav** » 13 Avr 2010, 11:26

On doit avoir

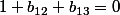
ce qui impose que

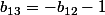
. En regardant "l'autre" diagonale on a que

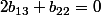
ce qui te permet d'exprimer

. Ensuite en regardant la deuxième ligne tu peux exprimer

puis à l'aide de la dernière colonne

.
Il faut maintenant te servir de la diagonale pour trouver la valeur de

.

par **Ben314** » 13 Avr 2010, 11:37

Ben... je trouve aussi une infinité de solutions (à vérifier) :

.
(c'est un espace affine)

Edit : Zut, j'ai encore mal lu l'énoncé. La matrice doit être symétrique...
donc une seule soluce avec x=-1...

par **girdav** » 13 Avr 2010, 11:39

Ben314 a écrit:Ben... je trouve aussi une infinité de solutions (à vérifier) :
.
(c'est un espace affine)

Mais il faut que la matrice soit en plus symétrique, ce qui fixe le

.

par **Ben314** » 13 Avr 2010, 11:41

Je vient juste de m'en rendre compte...
désolé.

par **sarah79** » 13 Avr 2010, 12:00

Je n'arrive pas à sortir le b12. Depuis ce matin je refais le système j'exprime les autre termes en fonction de b12, ça s'est pas trop dur mais je bloque pour trouvé le b12 malgré l'indication de me servir de la diagonale.

par **Ben314** » 13 Avr 2010, 12:02

Est tu sûre de ne pas avoir fait la même erreur que moi, c'est à dire "d'oublier" que la matrice doit être symétrique ?
Tu sait que b12=b21, que b13=b31...

par **sarah79** » 13 Avr 2010, 12:05

non je n'ai pas oublié j'ai travaillé avec la matrice:
( 1 b12 b13)
(b12 b22 b23)
(b13 b23 b33)

par **sarah79** » 13 Avr 2010, 19:07

quelqu'un peut-il m'aider?

par **girdav** » 13 Avr 2010, 20:52

Quelles sont les relations que tu trouves pour les autres coefficients?

par **sarah79** » 14 Avr 2010, 08:33

je trouve b13=-1-b12
b23=-2-3b12
b33=-3-2b12
b22=2+2b12
et après je suis bloqué donc pour trouver b12?

par **Ben314** » 14 Avr 2010, 09:05

Il semblerait qu'il te manque la troisième ligne (ou colonne) :
b13+b23+b33=0

par **sarah79** » 14 Avr 2010, 10:09

oui jai également b13+b23+b33=0 mais je ne vois pas a quoi elle me sert pour trouver b12.

par **Doraki** » 14 Avr 2010, 10:13

bah là-dedans tu peux remplacer b13, b23, et b33 par leur expression en fonction de b12. Ca te donnera une équation que b12 doit vérifier.

par **sarah79** » 14 Avr 2010, 10:28

Merci beaucoup j'avais pas pensé a faire ça je l'avais changé dans les autres mais du coup b12 disparaissait et jpouvais pas trouvé sa valeur. Là je trouve bien ce qu'il faut càd b12=-1. Merci encore.

Matrice magique symétrique

matrice magique symétrique

Qui est en ligne