Matrice jacobienne et continuité

[tilt77]

Bonjour
avec
f(a,b,c)->x= a sin b cos c; y= a sin b sin c, z= a cos b
je calcule le jacobien je trouve a²sinb
comment puis je montrer que la fonction
g(x,y,z)= [x²y+y²z+z²x]/ (x²+y²+z²)
est continue en (0,0,0)
si x; y et z sont différents de 0 sinon f(0,0,0)=0

[Ben314]

Pour f, c'est O.K. (en fait, c'est la fonction de "coordonnées sphériques")

Pour g, tu pose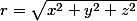 et, par définition, il faut montrer que g tend vers 0 lorsque r tend vers 0.
Ici, une simple majoration donne le résultat.

Indic : ne pas oublier que, |x| , |y| et |z| sont évidement inférieurs à r.

[tilt77]

bonjour
oui mais en utilisant le jocobien que j'ai calculer comment puis je montrer que g est continue?

[Ben314]

En utilisant le jacobien des coordonnées sphériques, ... je vois pas...

A la rigueur, en utilisant les coordonnées sphériques : ta fonction f avec pour ensemble de départ [0,oo[x[-pi/2,pi/2]x[-pi,pi] est surjective ce qui permet de dire qu'un (x,y,z) quelconque de R^3 peut s'écrire avec les formules que tu donne. En suite le 'r' dont je te parle (que l'on fait tendre vers 0), ben c'est ton 'a' donc il faut montrer que g tend vers 0 lorsque a tend vers 0.

Donc on peut utiliser les coordonnées sphériques (i.e. la fonction f) pour montrer que g est continue en 0 (mais c'est pas trés malin).