Matrice equivalente

[Maneeeel]

bonsoir ,
comment on peut determiner les matrices inversibles qui existe lorsque deux A et B matrice sont équivalente sachant A et B .
( sachant que A et B ne sont pas carre )
merci

[aviateur]

Bonjour
Je n'ai rien compris à la question. Suis-je bête ou quoi?

[Pseuda]

Bonjour aviateur,

Tu me rassures, je n'ai rien compris non plus, surtout pour parler de matrices inversibles s'agissant de matrices non carrées.

[Ben314]

Salut,
A mon avis, la question est la suivante :
Soient A et B deux matrices nxm (donc éventuellement non carrées) équivalentes, c'est à dire telles qu'il existe deux matrices inversibles P de taille nxn et Q de taille mxm telles que B=PAQ (i.e. A et B représentent la même application linéaire de R^m dans R^n, mais dans des bases différentes au départ et à l'arrivée et en fait, ça équivaut à dire que A et B ont le même rang)
Si on connait explicitement les matrices A et B (et qu'on sait qu'elles sont équivalentes), comment fait-on pour déterminer explicitement des matrices P et Q qui marchent ?

Exemple : Comment trouver le plus vite possible des ? tels que (il y a à plusieurs solutions)
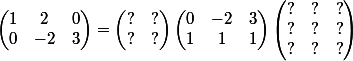(où la matrice 2x2 et la 3x3 doivent être inversibles)

Mais bon, vu le charabia complet de la question, on peut se demander si c'est bien ça le problème et j'ai pas envie de perdre mon temps pour répondre sachant que c'est peut être pas ça du tout le problème (sans parler du fait que Maneeeel, ça doit faire 20 fois qu'on lui dit de formuler ces question de façon à ce que ça veuille dire quelque chose et que ça semble être aussi utile que de p... dans un violon)

[Maneeeel]

je m 'excuse , c 'est ca la question je cherche les deux matrice inversible qui le vérifie ...