Matrice définie positive

[totor]

Bonjour,

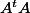
j'aimerais savoir si pour une matrice , la matrice est symmétrique et définie positive ? ou symmétrique et conditionnelement définie positive ?? est-ce vrai ? Sur les deux trois cas que j'ai testé les valeur propres ont l'air de ne pas être trop négatives :/

merci par avance!

ps : je suis nul en maths :hum:

[jose_latino]

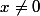
Si la matrice a une inverse, alors c'est vrai que . Une autre façon de dire qu'une matrice est positive est: si est symmétrique et , pour tout (définition plus générale, qui sert aussi pour le cas de dimension infinie). Alors, comme ça, c'est facile à vérifier que si a une inverse. :we:

[xon]

oui et si A n'est pas inversible tu gardes toujours le coté positif mais pas défine