Matrice : combinaison linéaire

[aymane]

Bonjour à tous. Je bloque sur une question d'un exercice de mathématiques concernant les combinaisons linéaires de matrices. J'espère que quelqu'un pourra m'aider.

"Soit A une matrice carrée d'ordre n ; on suppose que A² est une combinaison linéaire de A et In (où In matrice de l'identité n*n) : A²=aA+bIn.
1. Montrer que A^k est également combinaison linéaire de A et in pour tout k entier positif"

J'ai essayé de répondre à cette question en utilisant la récurrence pour k supérieur ou égal à deux (je traite le cas k=1 à part)
J'ai posé la propriété P(k): A^k = a(k-1)A + b(k-1)In

Initialisation :
Pour k=2 on a A² = a(2-1)A+b(2-1)In = aA+bIn
Ainsi P(2) vraie

Hérédité : (c'est là que je coince...)
Prouvons que A^(k+1) = akA + bkIn

A^(k+1) = A*A^k = A*(a(k-1)A+b(k-1)In) = ....
J'ai beau essayer de faire le calcul, je n'arrive pas au résultat souhaité... Quelqu'un pourrait t-il m'aider svp ?

Cas de k=1
J'ai également un souci : le calcul donne A=a*O*A+b*O*In=0*A+0*In...

Cordialement

[Pianoo]

Bonsoir,

Tu te compliques un peu.
Pour k=1 il n'y a rien à faire. c'est bien combinaison linéaire de A et de I.
Pour k=2 c'est ton donné dans l'énoncé il n'y a rien à faire.

Tu supposes la propriété vraie au rang k (k >= 2).

Hérédité :

Par hypothèse de récurrence au rang k,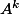 s'écrit donc
Il reste à ré-appliquer l'hypothèse de récurrence au rang k = 2 pour conclure.

[aymane]

Je ne comprend pas. Selon vous, on a A^k = aA+bIn. Or, selon l'énoncé, c'est A² qui est égal à aA+bIn...

Mon hypothèse de récurrence est-elle fausse ?

[Pianoo]

Je ne comprend pas. Selon vous, on a A^k = aA+bIn. Or, selon l'énoncé, c'est A² qui est égal à aA+bIn...

Mon hypothèse de récurrence est-elle fausse ?

Je n'ai pas affirmé que A^k = aA+bIn, mais il s'agit de mon hypothèse de récurrence au rang k.
En gros mon hypothèse de récurrence est : je suppose qu'il existe un k >= 2 tel que A^k s'écrive comme combinaison linéaire de A et de I.

Ton hypothèse de récurrence est fausse oui.
Tu peux faire un simple calcul pour le voir :
On a A² = aA + bI donc A^3 = aA² + bA = a(aA + bI) + bA = (a²+b)A + abI ce qui est différent de a(k-1)A + b(k-1)I.

J'ai pris comme hypothèse de récurrence au rang k :
"il existe et tels que "
C'est suffisant comme hypothèse puisqu'on ne te demande pas l'expression des coefficients (dans la combinaison linéaire).

Toi tu as essayé de prendre comme hypothèse de récurrence une expression qui te donnerais les coefficients en fonctions de a, b et de k pourquoi pas oui mais c'est plus compliqué.