Matrice circulante
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 21 Aoû 2014, 16:09
par Mikihisa » 21 Aoû 2014, 16:09
Bonjour je souhaite calculer le déterminant de la matrice suivante :

Voilà donc l'indication : utiliser la matrice
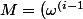(j-1)})_{1\leq i,j\leq n})
avec
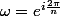
Donc on cherche en gros si j'ai bien compris a calculer det(AM) et det(M), pour AM je suis arriver a la conclusion que
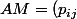_{1\leq i,j\leq n})
avec
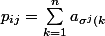}\omega^{(i-1)(k-1)})
où
=\left\{ \begin{array} n\text{ si k=1} \\ k-1\text{ si k\geq 2} \end{array}\right)
Et de plus je remarque bien que si (i-1)(j-1)>n on est ramener a une puissance de Omega <n (vu w^n=1), mais je n'arrive toujours pas a conclure avec tout ça

Des avis ?
Cordialement.
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 21 Aoû 2014, 16:20
par Mikihisa » 21 Aoû 2014, 16:20
:dodo: Ce que je voulais dire a la fin en écrivant le message c'que dans la matrice M chaque colonne est composer exactement des n puissance de oméga
En fait je dis une connerie je crois : avec n = 4 par exemple, la colonne 3 :
w^0=1
w^2=w^2
w^4=1
w^6=w^2
:mur:
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 22 Aoû 2014, 08:02
par jlb » 22 Aoû 2014, 08:02
Salut, une aide: ce polynôme doit te servir à résoudre ce pb!!
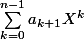
Sinon, une autre solution est de considérer la matrice et ses puissances successives
 \\<br />. &0 & 1 & (0) \\<br />. & . &. & . \\<br />. & . &. & . \\<br />0&.&.&1\\<br />1 & 0 & ... & 0<br />\end{matrix})
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 22 Aoû 2014, 16:39
par Mikihisa » 22 Aoû 2014, 16:39
Je rentre en L2 (oui je prend un peu d'avance) et je doit avouer que j'ai pas eu "trop" de problème en faisant le cours d'analyse, mais la j'me suis mis a l'algèbre, les généralité rappels ça pas de soucis, les forme multi-linéaire / det j'ai compris la construction et les méthodes de calculs, mais les vecteurs propres/polynome caractéristique/réduction je galère vraiment :-/
-
jlb
- Habitué(e)
- Messages: 1886
- Enregistré le: 27 Jan 2013, 17:35
-
 par jlb » 22 Aoû 2014, 20:54
par jlb » 22 Aoû 2014, 20:54
Du coup, regarde d'abord avec n=3, tu conserve tes a1,a2,a3, tu écris explicitement la matrice M, et tu calcules le produit. Après cela ne saute pas forcément aux yeux mais des petites factorisations DOIVENT te faire apparaître le polynôme indiqué évalué pour différentes valeurs. Après ce ne sont plus que des notions sur les déterminants à utiliser (multi linéarité, déterminant d'un produit et déterminant de Wandermonde).
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 22 Aoû 2014, 21:44
par Mikihisa » 22 Aoû 2014, 21:44
Ok je vais voir ça, merci !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
