Bonjour tout le monde
J'essaie de résoudre un cet exo mais j'ai du mal à le faire
Enoncé : Déterminer dans quel cas la matrice A est inversible ( A est une matrice carré d'ordre 3)
a b b
b a b
b b a
Mon soucis : Je sais qu'une matrice carré est inversible que lorsque son déterminant est non nul , en général , j'arrive à ma solution quand il y a un unique paramètre mais comment proceder avec 2 ?
Merci d'avance
Matrice carré , discussion , 2 paramètres
12 messages
- Page 1 sur 1
Re: Matrice carré , discussion , 2 paramètres
Bonjour
Tu calculs le déterminant en fonction de a et de b.
De toute façon si a=b la matrice est de rang 1, cela voudra dire que tu pourras mettre (a-b)^2 en facteur.
Tu calculs le déterminant en fonction de a et de b.
De toute façon si a=b la matrice est de rang 1, cela voudra dire que tu pourras mettre (a-b)^2 en facteur.
Re: Matrice carré , discussion , 2 paramètres
Salut,
Tu as une preuve (élémentaire) de ça ?aviateur a écrit:De toute façon si a=b la matrice est de rang 1, cela voudra dire que tu pourras mettre (a-b)^2 en facteur.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Matrice carré , discussion , 2 paramètres
il faudrait que tu y arrives avec 2 paramètres :
en développant par rapport à la première colonne : a(a²-b²)-b(...)+b(...)
la simplification se fait toute seule
variante :
(1)cas a= 0.
(2)sinon, tu divises par a toute la matrice et tu n'as plus qu'un seul paramètre : "b/a". Certes le déterminant est modifié, mais la résolution de det=0 ne change pas.
en développant par rapport à la première colonne : a(a²-b²)-b(...)+b(...)
la simplification se fait toute seule
variante :
(1)cas a= 0.
(2)sinon, tu divises par a toute la matrice et tu n'as plus qu'un seul paramètre : "b/a". Certes le déterminant est modifié, mais la résolution de det=0 ne change pas.
Re: Matrice carré , discussion , 2 paramètres
@ben j'ai déjà donné une preuve dans un post récent où la matrice était de de taille n (uniquement pour le déterminant) et où tu étais intervenu.
Ici c'est pas trop le but avec n=3 on peut calculer à la main et j'aide @gegetaka en lui faisant remarquer que l'on peut mettre (a-b)^2 en facteur c'est tout .
Pour moi le résultat est évident quand on est assez familiarisé avec les perturbations des opérateurs linéaires et une fois que l'on a vu qu'avec a=b la matrice est de rang 1.
(d'ailleurs je conseille de voir le livre de T. Kato, Perturbation Theory for Linear Operators, Classics in Mathematics, Springer-Verlag, New York (1980) qui est très bien fait puisque qu'il met le lecteur en confiance avec des tas d'exemples d'opérateurs en dim finie au début de son livre)
Maintenant on peut expliquer le résultat avec des arguments élémentaires: soit en raisonnant sur le polynôme homogène à 2 variables a et b qu'est le déterminant ou alors comme ci-dessous:
On note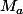 la matrice et
la matrice et 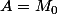
Det(M_a) c'est aussi) ou
ou 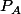 est le polynôme caractéristique de A.
est le polynôme caractéristique de A.
Mais c'est évident que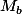 est de rang 1 ce qui est équivalent à dire que -b est valeur propre de A de multiplicité n-1. Mais tr(A)=0 donc la dernière valeur propre est (n-1) b (ici 2 b).
est de rang 1 ce qui est équivalent à dire que -b est valeur propre de A de multiplicité n-1. Mais tr(A)=0 donc la dernière valeur propre est (n-1) b (ici 2 b).
On en déduit donc=\pm (x+b)^{n-1} (x-(n-1) b)) et puis le déterminant de
et puis le déterminant de 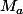
Ici c'est pas trop le but avec n=3 on peut calculer à la main et j'aide @gegetaka en lui faisant remarquer que l'on peut mettre (a-b)^2 en facteur c'est tout .
Pour moi le résultat est évident quand on est assez familiarisé avec les perturbations des opérateurs linéaires et une fois que l'on a vu qu'avec a=b la matrice est de rang 1.
(d'ailleurs je conseille de voir le livre de T. Kato, Perturbation Theory for Linear Operators, Classics in Mathematics, Springer-Verlag, New York (1980) qui est très bien fait puisque qu'il met le lecteur en confiance avec des tas d'exemples d'opérateurs en dim finie au début de son livre)
Maintenant on peut expliquer le résultat avec des arguments élémentaires: soit en raisonnant sur le polynôme homogène à 2 variables a et b qu'est le déterminant ou alors comme ci-dessous:
On note
Det(M_a) c'est aussi
Mais c'est évident que
On en déduit donc
Re: Matrice carré , discussion , 2 paramètres
Bonjour,
Pour Gegetaka : sur ce genre de problème, on peut parfois se simplifier la vie en observant les termes de la matrice : ici ils sont tous a ou b, leurs différences seront zéro ou a-b ( ou b-a = - (a-b) ).
Fait (par exemple) : colonne1-colonne3 et colonne2-colonne3, tu as vite un problème plus simple...
Cordialement
Rdvn
Pour Gegetaka : sur ce genre de problème, on peut parfois se simplifier la vie en observant les termes de la matrice : ici ils sont tous a ou b, leurs différences seront zéro ou a-b ( ou b-a = - (a-b) ).
Fait (par exemple) : colonne1-colonne3 et colonne2-colonne3, tu as vite un problème plus simple...
Cordialement
Rdvn
Re: Matrice carré , discussion , 2 paramètres
Bjr
RDvn, Evidemment pour @gegeteka on n'envisage pas autre chose que de lui suggérer de calculer le déterminant en lui indiquant simplement qu'elle doit voir dans son calcul une factorisation par (a-b).
Le reste de la discussion s'adresse à celui qui sait exactement ce qu'est une matrice carrée.
RDvn, Evidemment pour @gegeteka on n'envisage pas autre chose que de lui suggérer de calculer le déterminant en lui indiquant simplement qu'elle doit voir dans son calcul une factorisation par (a-b).
Le reste de la discussion s'adresse à celui qui sait exactement ce qu'est une matrice carrée.
Re: Matrice carré , discussion , 2 paramètres
Bonjour
Tout ceci n'était destiné qu'a orienter Gegetaka vers une méthode moins lourde que développer par colonne,
et permettant de voir le "pourquoi" de (a-b)^2, en restant dans l'élémentaire.
Cdlt
Rdvn
Tout ceci n'était destiné qu'a orienter Gegetaka vers une méthode moins lourde que développer par colonne,
et permettant de voir le "pourquoi" de (a-b)^2, en restant dans l'élémentaire.
Cdlt
Rdvn
Re: Matrice carré , discussion , 2 paramètres
Oui RDvn, on bien compris ce que tu dis: si on calcule le déterminant on obtient une forme développée et alors qu'il sera difficile d'arriver à la factoriser (car c'est cela que l'on veut pour arriver à voir quand il est nul).
Donc, il est préférable de faire comme tu dis, tes opérations sue les colonnes (ou lignes) de façon à chercher une factorisation a priori. Et c'est ça que @gegetaka devrait comprendre. Mais visiblement il y a un silence radio de son côté.
Donc, il est préférable de faire comme tu dis, tes opérations sue les colonnes (ou lignes) de façon à chercher une factorisation a priori. Et c'est ça que @gegetaka devrait comprendre. Mais visiblement il y a un silence radio de son côté.
Re: Matrice carré , discussion , 2 paramètres
Vu qu'il semblerais que @gegetaka ne soit plus là, je peut éventuellement poser la question telle qu'elle m'est venue à l'esprit en voyant le post d'aviateur :
Soit M(t) est une matrice carrés nxn dont les coeff. sont des polynômes en .
.
Si le rang de M(to) est n-2 peut-on en déduire [facilement ?] que déterminant de M(t) [qui est aussi un polynôme en t] est divisible par (t-to)^2 ?
n-2 peut-on en déduire [facilement ?] que déterminant de M(t) [qui est aussi un polynôme en t] est divisible par (t-to)^2 ?
Soit M(t) est une matrice carrés nxn dont les coeff. sont des polynômes en
Si le rang de M(to) est
Modifié en dernier par Ben314 le 09 Oct 2018, 13:55, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Matrice carré , discussion , 2 paramètres
C'est une bonne question. Je sais qu'avec le livre de Kato j'aurai pu te répondre rapidement car je suis sûr que c'est dedans. Malheureusement je ne l'ai plus en ma possession.
De toute façon tu veux une réponse avec des arguments simples, c'est à dire avec des connaissances de base.
Je pense que c'est possible et je vais y réfléchir plus tard. Je pense que c'est possible comme dans la situation précédente mais c'était une situation très simple.
Ceci étant dit. On se ramène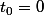 sans problème. Et on se place dans le corps des complexes.
sans problème. Et on se place dans le corps des complexes.
On désigne par M(z) la matrice de taille n (où si on veut l'opérateur linéaire qu'elle représente). Posons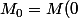) tes hypothèses sont que les coefficients de M(z) sont des polynômes en z, donc M(z) est analytique et
tes hypothèses sont que les coefficients de M(z) sont des polynômes en z, donc M(z) est analytique et  est de rang n-k (
est de rang n-k (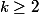 , 2 par exemple ) .
, 2 par exemple ) .
Moralement, une des idées de base que l'on trouve dans Kato c'est que le spectre de M(z) dépend continument de z.
C'est dire que si on désigne par,\lambda_2(z),...,\lambda_n(z))) le spectre de M(z) et bien le spectre de
le spectre de M(z) et bien le spectre de  c'est :
c'est :,\lambda_2(z),...,\lambda_n(z)))
Mais par hypothèse le rang de c'est
c'est 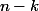 . C'est à dire que le noyau de
. C'est à dire que le noyau de  est de dimension k, i.e 0 comme valeur propre est de multiplicité au moins égale à k.
est de dimension k, i.e 0 comme valeur propre est de multiplicité au moins égale à k.
Le spectre de est donc de la forme
est donc de la forme ) après avoir arrangé convenablement le spectre de M(z)).
après avoir arrangé convenablement le spectre de M(z)).
On a alors)=\Prod_{i=1}^n (\lambda_i(z))) et donc, avec l'argument de continuité, on a bien que 0 est racine d'ordre au moins k.
et donc, avec l'argument de continuité, on a bien que 0 est racine d'ordre au moins k.
ceci répond en partie à ta question.
Reste à trouver des arguments simples qui sont à mon avis de passer par le fait que l'application) est analytique sur
est analytique sur 
De toute façon tu veux une réponse avec des arguments simples, c'est à dire avec des connaissances de base.
Je pense que c'est possible et je vais y réfléchir plus tard. Je pense que c'est possible comme dans la situation précédente mais c'était une situation très simple.
Ceci étant dit. On se ramène
On désigne par M(z) la matrice de taille n (où si on veut l'opérateur linéaire qu'elle représente). Posons
Moralement, une des idées de base que l'on trouve dans Kato c'est que le spectre de M(z) dépend continument de z.
C'est dire que si on désigne par
Mais par hypothèse le rang de
Le spectre de
On a alors
ceci répond en partie à ta question.
Reste à trouver des arguments simples qui sont à mon avis de passer par le fait que l'application
Re: Matrice carré , discussion , 2 paramètres
Bon, déjà, au moins au départ, je m'en fout un peu que ce soit "simple" où pas.
Donc par exemple là, que tu évoque que l'on peut suivre continuement les racines d'un polynômes à coeff. dépendant (continuement) d'un paramètre z, c'est clair que c'est pas du tout du "élémentaire", mais c'est pas grave.
Par contre, je suis quand même pas convaincu par ta preuve, plus précisément là :) sont continues, mais tu ne peut pas dire grand chose de plus (elle ne sont pas forcément dérivables en les points zo où le polynôme admet des racines multiples donc en particulier, il est très très peu probable qu'elle soit polynomiales en z).
sont continues, mais tu ne peut pas dire grand chose de plus (elle ne sont pas forcément dérivables en les points zo où le polynôme admet des racines multiples donc en particulier, il est très très peu probable qu'elle soit polynomiales en z).
Donc pourquoi n'aurait on pas (par exemple) un truc plus ou moins du style\!=\!\sqrt{|z|}) ;
; \!=\!\dfrac{z}{\sqrt{|z|}}) qui sont bien continue et nulle en 0 mais dont le produit est le polynôme
qui sont bien continue et nulle en 0 mais dont le produit est le polynôme  qui a 0 comme racine simple ?
qui a 0 comme racine simple ?
P.S. Je passe sur le sous-forum "énigme" : ça sera quand même mieux placé...
enigmes/rang-une-matrice-coefficients-variable-t198423.html
Donc par exemple là, que tu évoque que l'on peut suivre continuement les racines d'un polynômes à coeff. dépendant (continuement) d'un paramètre z, c'est clair que c'est pas du tout du "élémentaire", mais c'est pas grave.
Par contre, je suis quand même pas convaincu par ta preuve, plus précisément là :
Tes fonctionsaviateur a écrit:On a alorset donc, avec l'argument de continuité, on a bien que 0 est racine d'ordre au moins k.
Donc pourquoi n'aurait on pas (par exemple) un truc plus ou moins du style
P.S. Je passe sur le sous-forum "énigme" : ça sera quand même mieux placé...
enigmes/rang-une-matrice-coefficients-variable-t198423.html
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
