Matrice d'application linéaire

[Veelox]

Bonjour, jai vraiment un problème avec la question de construire une matrice d'application linéaire pour la projection sur la droite y=2x parallèlement à la droite y=3x. Schématiquement je comprend ce quil se passe cest le reste le probleme.

[Ben314]

<<<**********>>>
J'ai une fois de plus confondu "modifier" et "citer" et j'ai donc perdu ce message.
Et... j'ai la flemme de le retaper...
<<<**********>>>

[Veelox]

Je ne pense pas avoir compris, jai de la difficulté avec la notion dimage. Suis-je senser avoir trouver x+y et 3x+2y et ensuite resoudre?

[Ben314]

Avec les méthode proposées ci dessus, je vois pas bien à quel endroit tu aurais un système d'inconnues x et y à résoudre (avec d'autre méthodes, ça pourrait être le cas, mais pas là).
Les truc que tu cherche, c'est a,b,c,d.

Et la notion "d'image" y'a pas plus con : c'est le "résultat" que donne la fonction, c'est à dire que d'écrire "6 est l'image de 2 par la fonction x->3x" ben c'est complètement la même chose que d'écrire "6 c'est 3 fois 2".

Donc là, par exemple, l'énoncé te dit qu'on projette sur la droite y=2x et ça signifie que les projetés des vecteurs de cette droite, ben c'est eux même et ça, à peu prés tout le monde l'écrit "L'image d'un vecteur de cette droite, c'est lui même" (ca fait "plus joli").
Donc en terme de calcul, l'énoncé te dit que le projeté par exemple du vecteur (1,2), ben c'est le vecteur (1,2) [i.e. que l'image de (1,2) c'est (1,2)] et vu qu'on sait que la "formule" qui donne les coordonnées (x',y') du projeté d'un vecteur (x,y) et du type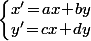 , ben ça signifie que 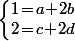(si (x,y)=(1,2) alors (x',y') est aussi égal à (1,2))
Ensuite, vu qu'on projette "parallèlement à y=3x", ça te dit quoi concernant le projeté de (1,3) [qui est sur la droite y=3x] ?

[Veelox]

Donc au final le y=3x me donnerait quelque chose qui ressemblerait à

[Ben314]

Bien sûr que non.
Lorsque tu projette SUR "truc" PARALLELEMENT à "bidule" ça me semble quand même être évident que "truc" et "bidule" ils jouent pas le même rôle là dedans, non ?

As tu fait un dessin pour comprendre de quoi il retourne ?
Sur ce dessin, tu lit quoi comme image de (1,3) ?

[Veelox]

Jai jamais au grand jamais eu de problème en mathématique calcul 1-2-3, 90% minimum, mais depuis que j'ai commence le cours d’algèbre linéaire je galère, pourtant ca ne fait que 4 semaine. La question qui ma ete donné en devoir, j'ai même été voir mon professeur qui ma pas expliqué grand chose, je n'ai jamais vue aucun exemple semblable dans un livre ou sur internet, seulement la projection orthogonal de un vecteur sur un la droite Ox ou Oy exemple. Je suis quelqun de visuel, je vois ce qu'il se passe sur un dessin, cest au niveau matriciel que sa bloque

[Pseuda]

Bonsoir,

Je vais essayer de t'aider. On cherche la matrice d'une application linéaire correspondant à une projection.

Donc on cherche a,b,c,d tels que l'image du vecteur (1,2) (qui porte la droite d'éq. y=2x) soit lui-même (car il est invariant par la projection sur lui-même), et que l'image du vecteur (1,3) (qui porte....) soit le vecteur nul (0,0).

Cela donne un système de 4 équations à 4 inconnues.

Je te conseille de faire un dessin d'une projection vectorielle sur une droite vectorielle //nt à une autre droite, pour bien te représenter ce que c'est (que devient un vecteur de chacune des 2 droites ?).

[Veelox]

Donc je cherche F (1,2)=1,2 et F (1,3)=0,0?

[Pseuda]

Si tu appelles F la matrice, c'est ça.

[Veelox]

Donc a=3, b=-1, c=6 et d=-2? Ce qui me donne ma matrice dapplication lineaire?

[Pseuda]

C'est bon. Pour vérifier ton résultat, tu peux "fabriquer" un vecteur somme d'un vecteur de la droite y=2x (par exemple (2,4)) et d'un vecteur de la droite y=3x (par exemple (-1,-3)) et vérufier que son image ne fait bien que le 1er vecteur.

[Veelox]

Merci beaucoup pour votre aide, un bel exemple de comment un question simle peut paraitre compliqier!

[Ben314]

Sinon, on pouvait aussi déterminer l'image d'un vecteur (x,y) quelconque.
Pour se faire, ben faut l'écrire comme la somme d'un vecteur V de la droite y=2x et d'un vecteur W de la droite y=3x et son projeté, ça sera V.
Donc il faut résoudre (x,y)=(t,2t)+(s,3s) où x et y sont des paramètres (i.e. connus) et où les inconnues sont s et t.
Aprés calculs, on trouve t=3x-y (et s=y-2x, mais ça on s'en fout) donc le projeté de (x,y) c'est
(x',y')=(t,2t)=(3x-y,6x-2y) et tu retrouve ta matrice.