Matrice anti-circulante
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 20 Déc 2013, 01:03
par barbu23 » 20 Déc 2013, 01:03
Pour

, je pose :
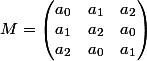
qu'on cherche à diagonaliser.
On pose :
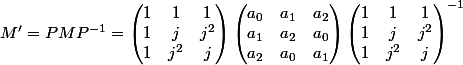
avec :

.

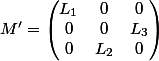
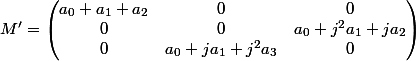
Est ce que c'est correct ?
Comment diagonaliser
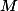
?
Edit : Je pense qu'il suffit de permuter de façon adéquate, les colonnes de la matrice
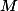
et celles de
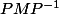
, pour aboutir à une matrice diagonale pour
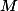
, mais comment ? :hein: , Bref, pas besoin de passer par la méthode traditionnelle qui consiste à trouver le polynôme caractéristique, espaces propres, ... etc.
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 20 Déc 2013, 07:51
par wserdx » 20 Déc 2013, 07:51
Bon tu as fait presque tout le travail. Comme expliqué sur le site wiki, les sous espaces stables de M' sont faciles à identifier. Il y a les espaces de dimensions 2 composés des vecteurs colonnes
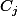
et
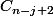
, le vecteur

tout seul et dans le cas où n est pair, il y en a un de plus, le vecteur
/2})
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 20 Déc 2013, 14:30
par barbu23 » 20 Déc 2013, 14:30
wserdx a écrit:Bon tu as fait presque tout le travail. Comme expliqué sur le site wiki, les sous espaces stables de M' sont faciles à identifier. Il y a les espaces de dimensions 2 composés des vecteurs colonnes
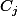
et
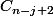
, le vecteur

tout seul et dans le cas où n est pair, il y en a un de plus, le vecteur
/2})
Merci beaucoup @wserdx. :happy3:
Comment faire pour la suite ? Comment diagonaliser
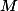
? En suivant la méthode que j'ai proposé ?
Merci d'avance. :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 24 Déc 2013, 11:14
par barbu23 » 24 Déc 2013, 11:14
wserdx a écrit:Bon tu as fait presque tout le travail. Comme expliqué sur le site wiki, les sous espaces stables de M' sont faciles à identifier. Il y a les espaces de dimensions 2 composés des vecteurs colonnes
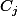
et
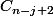
, le vecteur

tout seul et dans le cas où n est pair, il y en a un de plus, le vecteur
/2})
Merci beaucoup @wserdx. :happy3:
Comment faire pour la suite ? Comment diagonaliser
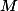
? En suivant la méthode que j'ai proposé ?
Merci d'avance. :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 27 Déc 2013, 00:26
par barbu23 » 27 Déc 2013, 00:26
svp, aidez moi à diagonaliser
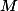
. :mur:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 27 Déc 2013, 16:29
par barbu23 » 27 Déc 2013, 16:29
Bonjour à tous,
On sait que :
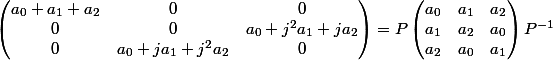
avec :
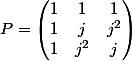
.
A quoi est égale

, matrice de passage, telle que :
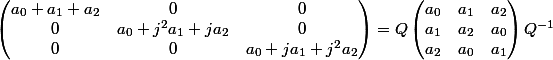
avec :
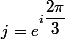
.
Je pense qu'il faut permuter les colonnes de la matrice de passage :
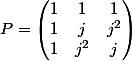
, mais, je ne sais pas comment.
Merci d'avance pour votre aide.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 14 invités
et
, le vecteur
tout seul et dans le cas où n est pair, il y en a un de plus, le vecteur
et
, le vecteur
tout seul et dans le cas où n est pair, il y en a un de plus, le vecteur