Matrice 3X3
20 messages
- Page 1 sur 1
Matrice 3X3
Bonjour,
j'ai une matrice A = 0 10 3
10 0 3
3 3 3
On me demande de trouver les valeurs et vecteurs propres de A
pour cela j'effectue det(A-XI): (0-µ) 10 3
10 (0-µ) 3
3 3 (3-µ)
j'obtiens ensuite (3-µ).[(0-µ).(0-µ).100] = 300µ²-100µ³
est-ce correct jusqu'ici?
si oui arrivée à cette solution que fais-je pour trouver les valeurs propres de µ? Horner?
j'ai une matrice A = 0 10 3
10 0 3
3 3 3
On me demande de trouver les valeurs et vecteurs propres de A
pour cela j'effectue det(A-XI): (0-µ) 10 3
10 (0-µ) 3
3 3 (3-µ)
j'obtiens ensuite (3-µ).[(0-µ).(0-µ).100] = 300µ²-100µ³
est-ce correct jusqu'ici?
si oui arrivée à cette solution que fais-je pour trouver les valeurs propres de µ? Horner?
Salut,
quel est le rapport entre les valeurs propres de A et le déterminant de A-XI? A ton niveau, le but quand on apprend une méthode n'est pas de la retenir par coeur mais de la comprendre. Ici, tu ne sembles pas comprendre ce que tu fais, et le pire et qu' apparemment tu ne connais même pas la méthode par coeur...
quel est le rapport entre les valeurs propres de A et le déterminant de A-XI? A ton niveau, le but quand on apprend une méthode n'est pas de la retenir par coeur mais de la comprendre. Ici, tu ne sembles pas comprendre ce que tu fais, et le pire et qu' apparemment tu ne connais même pas la méthode par coeur...
oui effectivement, je n'ai pas de cours théorique pour m'appuyer pour faire les exercices donc je cherche sur internet à comprendre mes exercices et essaye de mémoriser la méthode même si ce n'est pas la meilleure solution.
et de ce qui est pour la question:
quel est le rapport entre les valeurs propres de A et le déterminant de A-XI?
pour moi, lorsque j'effectue une matrice pour trouver ces valeurs propres j'utilise le det, mais je peux me tromper évidemment
et de ce qui est pour la question:
quel est le rapport entre les valeurs propres de A et le déterminant de A-XI?
pour moi, lorsque j'effectue une matrice pour trouver ces valeurs propres j'utilise le det, mais je peux me tromper évidemment
Chercher les valeurs propres ça revient en fait à chercher un élément Lambda de R tel qu'il existe un vecteur v non nul de sorte que A.v = Lambda.v
C'est à dire que v appartient au noyau de A-Lambda.Id. Ainsi ce noyau n'est pas réduit au vecteur nul et donc la matrice A-Lambda.Id n'est pas inversible.
Mais on sait qu'une matrice n'est pas inversible si et seulement si son déterminant est non nul. C'est pour ça qu'on instaure le polynôme caractéristique et c'est pour ça que les valeurs propres sont exactement les racines de ce polynôme. Donc essaye de trouver les racines en factorisant ton polynôme.
C'est à dire que v appartient au noyau de A-Lambda.Id. Ainsi ce noyau n'est pas réduit au vecteur nul et donc la matrice A-Lambda.Id n'est pas inversible.
Mais on sait qu'une matrice n'est pas inversible si et seulement si son déterminant est non nul. C'est pour ça qu'on instaure le polynôme caractéristique et c'est pour ça que les valeurs propres sont exactement les racines de ce polynôme. Donc essaye de trouver les racines en factorisant ton polynôme.
Oui, c'est ça.
Il ne te reste plus qu'a résoudre les deux systèmes correspondant à AX=0X et à AX=3X pour trouver les vecteurs propres associés à tes deux valeurs propres 0 et 3.
Edit : aprés vérification, je pense que tu t'est trompé dans ton déterminant : les valeurs propres sont -10 ; 1 et 12...
Il ne te reste plus qu'a résoudre les deux systèmes correspondant à AX=0X et à AX=3X pour trouver les vecteurs propres associés à tes deux valeurs propres 0 et 3.
Edit : aprés vérification, je pense que tu t'est trompé dans ton déterminant : les valeurs propres sont -10 ; 1 et 12...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Tient, comme j'ai 5mn, je vais te le calculer en essayant de faire le tour des opérations que l'on peut faire :
)
Cela ne change pas le déterinant d'ajouter à une ligne (resp. une colonne) un certain nombre de fois une autre ligne (resp/ colonne). Ici, si je retranche la deuxième ligne à la première, j'obtient :
)
On peut factoriser un élément qui apparait dans toute une ligne ou toute une colonne. Ici, par exemple, on a :
\,\det\left( \matrix{-1& 1 &0\cr 10& -\mu& 3\cr 3 &3 &3-\mu}\right))
Ici, le plus simple serait évidement d'ajouter la première colonne à la deuxième pour faire apparaitre un 0, mais, pour varier, on va développer ce determinant par rapport à la troisième colonne :
\Big[ +0\times \det\left( \matrix{ 10& -\mu\cr 3 &3 }\right)-3\times \det\left( \matrix{ -1& 1\cr 3 &3 }\right)+(3-\mu)\times \det\left( \matrix{ -1&1\cr 10& -\mu}\right)\Big])
Enfin on développe les petits déterminants 2x2 à l'aide de la formule bien connue :=ad-bc) :
:
\Big[ -3\times(-6)+(3-\mu)\times(\mu-10)\Big])
Enfin, il faut factoriser pour avoir les valeurs propres :
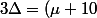( -\mu^2+13\mu -12) = (\mu+10)(\mu-1)(-\mu+12)= -(\mu+10)(\mu-1)(\mu-12))
Cela ne change pas le déterinant d'ajouter à une ligne (resp. une colonne) un certain nombre de fois une autre ligne (resp/ colonne). Ici, si je retranche la deuxième ligne à la première, j'obtient :
On peut factoriser un élément qui apparait dans toute une ligne ou toute une colonne. Ici, par exemple, on a :
Ici, le plus simple serait évidement d'ajouter la première colonne à la deuxième pour faire apparaitre un 0, mais, pour varier, on va développer ce determinant par rapport à la troisième colonne :
Enfin on développe les petits déterminants 2x2 à l'aide de la formule bien connue :
Enfin, il faut factoriser pour avoir les valeurs propres :
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
merci beaucoup j'ai bien compris la méthode,
mais j'ai une derniere question avant de poursuivre l'exercice, pourquoi dans un de mes exercices sur les matrices j'ai du aussi calculer les valeurs propres de A:
1 2 -4
4 -1 0
0 0 2
je fais bien évidemment
(1-µ) 2 -4
4 (-1-µ) 2
0 0 (2-µ)
et ensuite directement : (2-µ)[(1-µ)(-1-µ)-(4x2)]
ensuite factorisation et valeur propre
pourquoi je n'ai pas du passer par les autres étapes de l'autre calcul?
mais j'ai une derniere question avant de poursuivre l'exercice, pourquoi dans un de mes exercices sur les matrices j'ai du aussi calculer les valeurs propres de A:
1 2 -4
4 -1 0
0 0 2
je fais bien évidemment
(1-µ) 2 -4
4 (-1-µ) 2
0 0 (2-µ)
et ensuite directement : (2-µ)[(1-µ)(-1-µ)-(4x2)]
ensuite factorisation et valeur propre
pourquoi je n'ai pas du passer par les autres étapes de l'autre calcul?
Il faut bien te dire que les diff"rentes méthodes de mon post précédent ne sont pas obligatoire.
On pourrait systématiquement développer ou bien systématiquement faire de combinaisons de lignes ou bien systématiquement faire des combinaisons linéaires sur les colonnes.
Ce qu'il faut ce dire, c'est que, comme tout ce qui est "systématique", eh ben... c'est pas malin du tout.
La "bonne" méthode, c'est de bien regarder la matrice puis, en fonction de la "tête" qu'elle a, employer telle ou telle méthode...
Avec la matrice A de ton dernier post, y'a pas à hésiter : on développe par rapport à la troisième ligne vu qu'il y a déjà deux 0 dedans.
On trouve immédiatement... ce qu'il faut.
On pourrait systématiquement développer ou bien systématiquement faire de combinaisons de lignes ou bien systématiquement faire des combinaisons linéaires sur les colonnes.
Ce qu'il faut ce dire, c'est que, comme tout ce qui est "systématique", eh ben... c'est pas malin du tout.
La "bonne" méthode, c'est de bien regarder la matrice puis, en fonction de la "tête" qu'elle a, employer telle ou telle méthode...
Avec la matrice A de ton dernier post, y'a pas à hésiter : on développe par rapport à la troisième ligne vu qu'il y a déjà deux 0 dedans.
On trouve immédiatement... ce qu'il faut.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Pour le "produit d'Hadamard", y'a fallut que j'aille chercher sous google pour savoir ce que c'était....
En ce qui me concerne, je m'en suis jamais servi... (peut-être pour des casse tête) vu que je vois pas trop à quelle structure mathématique interessante ça correspond.
Résumé : à moins que tu ne fasse des maths appliqués à un truc un peu bizare ou bien qu'il y ait un truc précis dans l'énoncé qui dit de faire autrement, le produit de deux matrices, c'est toujours le produit ligne par colonne qui correspond à la composition des applications linéaires.
Ce produit est associatif, ce qui veut dire que A(BC)=(AB)C
mais il n'est quasi jamais commutatif : AB est différent de BA.
P.S. t'en a entendu parler où du "produit d'Hadamard" ?
En ce qui me concerne, je m'en suis jamais servi... (peut-être pour des casse tête) vu que je vois pas trop à quelle structure mathématique interessante ça correspond.
Résumé : à moins que tu ne fasse des maths appliqués à un truc un peu bizare ou bien qu'il y ait un truc précis dans l'énoncé qui dit de faire autrement, le produit de deux matrices, c'est toujours le produit ligne par colonne qui correspond à la composition des applications linéaires.
Ce produit est associatif, ce qui veut dire que A(BC)=(AB)C
mais il n'est quasi jamais commutatif : AB est différent de BA.
P.S. t'en a entendu parler où du "produit d'Hadamard" ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bon, fait gaffe quand même, j'y connait absolument rien du tout en "bioingénieur" donc peut être que le "produit d'Hadamard" y a des applications... (tu demendera à to prof. si tu y pense)
C'est (évidement) pas parce que je sais pas à quoi ça peut servir que ça sert à rien....
P.S. Pour ceux qui ont la flemme de chercher sous Google : le "produit d'Hadamard" ça consiste à faire le produit "terme à terme" des deux matrices.
Si y'en a qui savent à quoi ça peut servir en "BA1 bioingénieur" ben... y peuvent le dire...
C'est (évidement) pas parce que je sais pas à quoi ça peut servir que ça sert à rien....
P.S. Pour ceux qui ont la flemme de chercher sous Google : le "produit d'Hadamard" ça consiste à faire le produit "terme à terme" des deux matrices.
Si y'en a qui savent à quoi ça peut servir en "BA1 bioingénieur" ben... y peuvent le dire...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
