Maths: Dérivée d'ordre n

[mekodi]

Bonjour,

est- ce que quelqu'un pourrait m'aider sur un exercice sur la dérivée d'ordre

il faut calculer la dérivée d'ordre n de f(x)=x^a avec x>0 et a non nul.

Est-ce que quelqu'un pourrait m'aider?
Merci d'avance

[girdav]

Vu que le fait de dériver une fois fait baisser de la puissance, on peut chercher la dérivée -ième sous la forme .

[mekodi]

Est ce que vous pourriez être plus précis svp?

[Ben314]

Salut,
As tu au moins calculé la dérivée d'ordre 1 ? celle d'ordre 2 ? celle d'ordre 3 ?

[girdav]

Est ce que vous pourriez être plus précis svp?

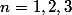
Là j'ai presque donné la réponse, donc je ne peux pas sans enfreindre la charte. Comme te le suggère Ben314, tu peux commencer par calculer à la main pour et commencer à conjecturer la formule.

[mekodi]

J'ai réussi a calculer la dérivée d'ordre 1, d'ordre 2 et d'ordre 3 dans problème c'est après pour pouvoir trouver la forme debla dérivée de f d'ordre n

[girdav]

Tu constates que la puissance de diminue de à chaque fois que tu dérives. Donc si tu dérives n fois tu a la puissance de départ moins n. Mais tu as aussi remarqué qu'il y a des "trucs qui tombent" quand tu dérives. Il reste à les identifier.

[mekodi]

Il reste à les identifier.

C'est justement ça où j'ai du mal. Lorsque je dérive une première fois, puis une dexième je me rend compte que f ''(x)=a*(a-1)^(a-2)...

Comment je peux faire pour trouver la dérivée d'ordre n sachant qu'il y a une partie constituée de x^(a-n)

[mekodi]

Il reste à les identifier.

C'est justement ça où j'ai du mal. Lorsque je dérive une première fois, puis une dexième je me rend compte que f ''(x)=a*(a-1)^(a-2)...

Comment je peux faire pour trouver la dérivée d'ordre n sachant qu'il y a une partie constituée de x^(a-n)

[mekodi]

Dois-je rajouter a! devant x^(a-1) ou ce n'est pas bon??