L3 math theorie des anneaux

[Dens]

Bonjour, je suis étudiant en mathématique,
Je bloque sur une question depuis plusieurs jours.
a,b appartient à Z m appartient àC\Z. a’b’ appartient à Q.
A= a+bm
K=a’+b’m
Montrer que si L un sous corps de C contenant A alors K inclus dans A. On dit que K est le corps des fractions de A dans C

Dans les question précédente j’ai montré que K est un sous Q espace vectoriel de C et est un sous corps de C contenant A

Dans mon cours le lien que jai pus trouver est:

que si L est un sous corps de C alors L est integre car C est un coprs

[GaBuZoMeu]

Tu voulais dire que A est l'ensemble des a + bm pour a et b entiers relatifs ? Alors ce que tu as écrit est incorrect.
Et ton paragraphe

Montrer que si L un sous corps de C contenant A alors K inclus dans A. On dit que K est le corps des fractions de A dans C

ne tient pas debout. Ou alors m n'est pas n'importe quoi ? (Par exemple son carré est rationnel ?)
Donne-nous plutôt ton énoncé complet, parce que ce que tu racontes ici est incohérent.

[Dens]

m appartient a C\Z tel que m^2-sm+p=0
Avec s,p appartient a Z

A=Z[m]=a+bm. Z[m] est sous anneau de C
K=Q[m]=a’+b’m.

[GaBuZoMeu]

Bon, tu avais juste oublié l'information essentielle sur m.
Et tu persistes à écrire de manière incorrecte A=a+bm alors que A={a+bm | a,b dans Z} (je t'ai déjà averti là-dessus).

Indications :
Tout sous corps de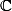 contient .
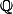Tout sous-corps de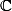 qui contient contient .