Dm math cardinal

[yoshiop]

bonjour

je bloque sur cette exercice de mon dm pouvez vous m'aidez svp

On considère G={1,2} X {1,2} et l'application définie par f : G → N*, (x,y) → 3x+y

1) quel est le cardinal de l'ensemble G ?
2) l'application est-elle surjective? injective ?

je sais que le cardinal c'est [|n|]={k∈N ; 1<k<n}
je vois pas comment appliquer à cause du "X"

ensuite avec un dessin je pence qu'elle est injective et non surjective

merci

[capitaine nuggets]

Salut !

Dit autrement, est l'ensemble des couples , où et . Combien de valeurs différentes peut prendre l'élément ? Combien de valeurs différentes peut prendre l'élément ? Combien de couples différent peut-on alors former ?

2. Par définition, l'application est surjective si, quel que soit l'entier naturel non nul qu'on se donne à l'ensemble d'arrivée, on peut toujours trouver au moins un antécédent par , c'est-à-dire . Or quelle différence y a-t-il entre les ensemble et ?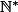

Toujours par définition, est injective si deux éléments distincts et de l'ensemble de départ ont des images différentes par , c'est-à-dire que si l'on suppose alors on a . Ce n'est pas trop difficile de vérifier si c'est le cas ou non