Majoration du reste serie alternée (critère spécial leibniz

[oubah]

Bonjour je suis bloqué depuis un certain moment sur une démo :

S = (-1)^n vn, ou Vn est une suite décroissante qui tend vers zéro.

Alors les deux sommes partielles S(2n) et S(2n+1) sont adjacentes. D'ou S(2n) converge => D'ou la somme converge vers S sa somme.


Donc j'arrive à : S(2n+1) S S(2n) pour tout n.

Et S= Sn + Rn donc j'obtiens juste que :

0 R(2n) -V(2n+1) et 0 R(2n+1) V(2n+1)



Mais je vois pas comment je peux dire que |Rn|<V(n+1)

Je vous remercie bonnes fêtes =)

[aymanemaysae]

Je pense que cette page satisfera votre curiosité sur ce sujet.

[oubah]

Merci, malheureusement la conclusion de la démo d unisciel est obscure

[Robot]

j'obtiens juste que :
0 R(2n) -V(2n+1) et 0 R(2n+1) V(2n+1)
Mais je vois pas comment je peux dire que |Rn|<V(n+1)

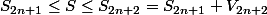
Pour le deuxième cas, tu peux faire mieux : puisque , on a

Soit un entier quelconque.
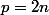
Si ( est pair), on a et donc .
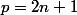
Si ( est impair), on a et donc .
En conclusion, pour tout entier on a .