Majoration d'un polynome

[hub974]

Bonjour
Je n'arrive pas à démontrer la formule suivante :
On note la fonction définie par :
Montrer l'existence d'un réel vérifiant :
Merci pour votre aide

[Mimosa]

Bonjour

D'abord il me semble qu'il y a un problème d'énoncé. ne peut pas être négatif!
Ensuite, dans le cas où commence par montrer que convient pour , ensuite essaye par récurrence sur .

[zygomatique]

salut

il ne me semble pas que x soit un problème : Q_k est pair et positif sur R+ ...

[Mimosa]

Oui, bien sur, tu as raison!

[zygomatique]

Q est pair donc on peut travailler sur R+ et est minimal en 0 ...

une idée ...

Q(0) = 1

et

or on cherche M tel que

[Ben314]

Salut,
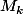
Si on veut, on peut trouver des constantes plus ou moins explicite pour les , mais si on réfléchi un peu, il y a aussi un argument assez trivial montrant l'existence du bidule et ne nécessitant comme seul "calcul" la constatation que pour tout .

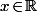
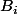
Donc pour tout , la fraction rationnelle est définie et continue sur . De plus, pour vu que le numérateur est de degré strictement plus petit que le dénominateur, la fraction tend vers zéro lorsque ce qui prouve qu'elle est bornée par un certain sur (et pour la fraction vaut 1 donc est bornée par ).
Et pour avoir le résultat, il suffit de prendre

[Lostounet]

Salut Ben,

Comment peut-on expliciter ces Mk ? Quelle serait ta méthode? Ça m'intéresse (j'ai pas trouvé...)

[Ben314]

Si alors, pour tout , on a
donc . Ensuite,
- Si est pair, on a trivialement
.
- Si est impair, on a
lorsque
mais aussi
lorsque
Donc dans tout les cas, on a pour tout ce qui signifie que convient et on peut éventuellement faire une étude de variation pour (peut-être) déterminer quel est le maximum des .

EDIT : En fait, de façon assez évidente, le max est obtenu pour donc convient.

[Lostounet]

Merci Ben ! Je vais lire ça.