Majoration d'intégrale

[tonythx]

Bonjour.

Dans le cadre du théorème de Lax milgram, j'ai besoin de montrer que:

sachant que A est une matrice définie positive...

Je vous serais reconnaissant de bien vouloir m'aider.
Merci beaucoup

[fahr451]

bonjour

une intégrale sans borne n'a pas grand sens de plus par rapport à quoi intègre-t-on?

il faudrait un énoncé un peu précis

[tonythx]

Désolé pour l'imprécision de l'énoncé, mais je pensais qu'on pouvait
minorer directement cette intégrale en utilisant le fait que A est définie
positif.
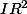
L'énoncé précise que l'on se trouve sur un ouvert de polygonal. De plus sur la frontière de cet ouvert
u=0.
Ainsi comment retrouve-t-on l'inégalité :

[Lead]

Je me demande si ya pas un théorème quelque part qui dit que:


avec x valant n'importe quoi (une expression mathématique)
En tout cas je sais que j'utilise tout le temps cette propriété(a moins que la norme soit supérieure à l'intégrale, je sais plus).

[tonythx]

je vois ce que tu veux dire, en fait il s'agit de l'autre sens car:
par le thm de cauchy schwarz on a:

(norme 2 bien sur)

[fahr451]

humm
ce qui serait bien aussi c'est qu'on sache ce qu 'est u d e façon précise

régularité ...

d'autre part dans ton post précédent pourquoi la norme de 1 serait elle égale à 1 ?