Majoration complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 07 Jan 2010, 16:53
par Nightmare » 07 Jan 2010, 16:53
Salut à tous !
Que dire d'une fonction
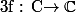
entière, nulle sur
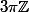
et majorée en tout point z complexe par
|})
?
Bonne réflexion
:happy3:
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 07 Jan 2010, 20:13
par ffpower » 07 Jan 2010, 20:13
Salut! ca me rappelle le théo du sinus ca:
Si f de R dans R est C infinie, si toutes les dérivées de f en 0 sont en valeur absolue inferieures a 1, et si f'(0)=1, alors f=sin..

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Jan 2010, 20:19
par Ben314 » 07 Jan 2010, 20:19
Je tente le coup...
Comme

s'annule sur
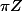
,
={f(z)\over\sin(z)})
est holomorphe sur
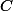
(i.e. entière)
Or, si
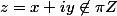
, on a
|=\frac{|f(z)|}{\sqrt{\sin^2(x)+\sinh^2(y)}} \leq \frac{\exp(|y|)}{\sqrt{\sin^2(x)+\sinh^2(y)}})
En utilisant un carré centré en 0 de coté
\pi)
(
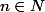
) et le fait que le max (en module) est au bord, je pense en déduire que

est bornée donc constante.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 07 Jan 2010, 20:22
par yos » 07 Jan 2010, 20:22
Salut.
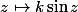
convient si
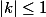
.
Inversement, on pose
=\frac{f(z)}{\sin z})
. Si on montre que g est entière et bornée, c'est fini par Liouville.
C'est assez évident qu'elle est entière...
montrons qu'elle est bornée : pour
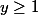
,
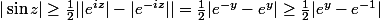
, et pareil pour
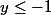
.
Dans la bande -1<y<1, il peut pas y avoir de maximum par le principe du maximum (hum : dernier point à vérifier).
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 07 Jan 2010, 20:24
par yos » 07 Jan 2010, 20:24
Grillé par Ben...
A Jord de trancher.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 07 Jan 2010, 20:33
par Nightmare » 07 Jan 2010, 20:33
Salut à vous deux !
J'ai essayé de montrer comme vous qu'elle était bornée, mais j'ai bloqué comme Yos sur la bande -1 <y <1 et je n'ai pas réussi à conclure avec le le principe du maximum.
Je m'en suis sorti autrement, en considérant non pas f(z)/sin(z) mais
}{sin(z)}\cdot \frac{1}{(\omega-z)^{2}})
avec
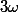
fixé dans
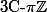
.
On a un résultat assez intéressant en calculant l'intégrale de ce machin là sur un cercle de rayon
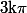
où k est à déterminer.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Jan 2010, 20:37
par Ben314 » 07 Jan 2010, 20:37
Il me semble que, la fonction
}{\sqrt{\sin^2(x)+\sinh^2(y)}})
est bornée sur les bords des carrés de coté
\pi)
(
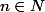
) et, en utilisant le principe du module maximum (il me semble que c'est comme cela que ça s'appelle) on conclue.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 07 Jan 2010, 21:15
par Nightmare » 07 Jan 2010, 21:15
Ben314 a écrit:Il me semble que, la fonction
}{\sqrt{\sin^2(x)+\sinh^2(y)}})
est bornée sur les bords des carrés de coté
\pi)
(
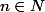
) et, en utilisant le principe du module maximum (il me semble que c'est comme cela que ça s'appelle) on conclue.
C'est ok pour moi. Astucieux le choix du carré !
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 16 Jan 2010, 15:06
par ffpower » 16 Jan 2010, 15:06
Salut!
Night, est ce que tu connaissais la démonstration du théo du sinus que j ai énoncé plus haut?(rms peut etre).
Car la méthode que tu utilises est quasi isomorphe a la méthode utilisée pour la démo de ce théoreme.
Si ce n est pas le cas, je peux expliquer comment faire, car la tous les préliminaires ont été fait^^
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 16 Jan 2010, 15:18
par Nightmare » 16 Jan 2010, 15:18
Salut ffpower :happy3:
J'avais proposé l'exercice dont tu parles sur le forum il y a pas si longtemps. En posant
}(0))
, F vérifie l'énoncé de mon premier post et coïncide sur R avec f. C'était donc effectivement les même méthodes :lol3:
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 16 Jan 2010, 15:20
par ffpower » 16 Jan 2010, 15:20
Oki...
( je sais pas quoi dire d autre XD)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités