Majorant d'une suite de fonction

[Als128]

Bonjour,

J'ai besoin d'un petit coup de pouce pour la majoration d'une suite de fonction.
Je dois majorer :
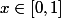
pour par une fonction lebesgue intégrable indépendante de n. La soluce donne mais je tourne en rond et j'arrive pas à retrouver ce resultat

Un petit coup de main ne serait donc pas de refus
Merci

[Ben314]

Salut,
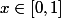
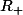
Peut être devrait tu, pour fixé, étudier la fonction sur , en particulier déterminer le maximum de cette fonction...

Par contre, je ne trouve pas le même majorant que toi...

[Dihtbscii]

Pour x=0 ça va être dure de majorer n^(3/2) par une fonction qui ne depend pas de n non?

[Ben314]

Pour x=0 ça va être dure de majorer n^(3/2) par une fonction qui ne depend pas de n non?

Ce n'est pas vraiment un problème : il veut majorer sa fonction par une fonction f lebesgue intégrable sur [0,1] et rien n'empèche de prendre
f(0)=+oo.

Par contre, le majorant que j'obtient (et qui n'est pas franchement améliorable) est qui n'est pas lebesgue intégrable au voisinage de 0.

On peut aussi voir que ça déconne en vérifiant que la limite des intégrales des fn n'est pas égal à l'intégrale de la limite (simple) des fn...

Edit : Je voterais assez fort pour une erreur d'énoncé du style

[alavacommejetepousse]

bonjour
sans calcul
de la forme

x^(-3/2) h (nx) avec h bornée donc bien de la forme de ben