Bonjout tout le monde !
Alors voilà depuis quelques temps je me pose la question suivante (peut-être qu'elle relève davantage de la section défi&énigmes, je ne sais pas...).
On prend

préhilbertien,

une partie

connexe par arcs de

.
On note
)
la borne inférieure des longueurs des arcs


à valeurs dans

reliant

à

,c'est à dire ici que
)
, que
=x)
et que
=y)
. La longueur

d'un arc
)
est ici définie au sens classique du terme, c'est à dire
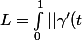||dt)
.
Il est clair que l'on peut trouver des ensembles

admettant au moins un bi-point
)
tel que
)
ne soit pas un minimum.
Ma question : existe-t-il

(non réduite à un point) tel que pour tout bipoint
)
avec

différent de

cette longueur ne soit pas atteinte ?
Bien-sûr vous pouvez modifier un peu l'énoncer si ça vous arrange, prendre les arcs

par morceaux, se placer dans un espace de dimension finie voire même dans le plan


